Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 미적분 #접선의 방정식 #최적화 #뉴턴법 #뉴턴-랩슨법
- 수리통계
- 시계열분석 #Time-Series Analysis #이상탐지 #Anomaly Detection #Spectral Residual #CNN #SR-CNN
- 미적분
- 프로그래머를 위한 선형대수 #선형대수 #고유분해 #고윳값 #고유벡터
- 프로그래머를 위한 선형대수 #선형대수 #행렬계산
- 미적분 #사인과 코사인의 도함수
- lightweightmmm
- Media Mix Modeling
- Marketing Mix Modeling
- Optimization
- 프로그래머를 위한 선형대수 #선형대수 #LU분해
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #야코비 회전법 #QR법 #하우스홀더반사 #행렬회전
- mmm
- 미적분 #평균값 정리 #로피탈의 정리 #접선의 방정식
- bayesian inference
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #고유분해
- bayesian
Archives
- Today
- Total
문과생 네버랜드의 데이터 창고
LightWeightMMM 리뷰 : Bayesian Methods for Media Mix Modeling with Carryover and Shape Effects(1) 본문
논문 Review
LightWeightMMM 리뷰 : Bayesian Methods for Media Mix Modeling with Carryover and Shape Effects(1)
K JI 2023. 11. 18. 18:16
<수정사항>
2024-12-16 채택 - 기각 알고리즘에 대한 내용 추가
<요약>
- Marketing mix Modeling(MMM)이란 각 매체별로 예산 분배를 최적화하고, 그 성과를 예측하는 마케팅 방법론을 의미한다.
1) 예산 분배 최적화란 광고를 집행하고자 하는 각 매체별로 얼마만큼의 예산분배를 해야 최대의 KPI를 달성하는지 고민하는 문제이다
2) 성과 예측이란 분배 최적화된 결과물을 가지고 얼마만큼의 성과를 거둘 수 있을 것인가 예측하는 분야를 말한다. - 다음의 절차를 거쳐 Marketing Mix Modeling을 수행하는 lightweightmmm을 제안한다.
1) 베이지안 회귀모델 적합
${(1)}$ 광고비 지출에 대한 성과가 시차를 두고 누적해서 나타나는 현상을 Carryover라고 하는데, 이를 모델링하는 carryover 함수를 적용한다
${(2)}$ 한계체감 성질을 모델링하는 $\beta Hill$ 함수를 적용한다.
${(3)}$ KPI Y값과, 외부요인 Z를 포함한 회귀 모델을 정의하고, Carrover, $\beta$hill, 회귀모델 파라미터를 MCMC 방법론을 통해 최적화한다.
2) 회귀모델 기반 최적 예산 믹스 도출 및 성과지표 측정
${(1)}$ ROAS를 계산한다.
${(2)}$ SLSQP라는 QP 알고리즘을 통해 예산 분배 최적해를 도출한다.
LightWeightMMM 알고리즘 얼개도
3. 데이터 전처리를 위한 컨볼루션 함수를 다양하게 변경하고, 베이지안 추론을 수행할 때 활용하는 사전분포를 바꾸는 행위는 모델의 성능에 상대적으로 큰 영향을 끼치는 것을 실험을 통해 보여준다.(2편에서 이를 다루고자 한다)
<본문>
- 서론
1) MMM이란 무엇인가?
${(1)}$ Marketing Mix Modeling : 예산 분배 최적 할당 도출 및 성과 예측
-. Media Mix Modeling이라고도 불리우는 Marketing Mix Modeling은 다음의 문제를 연구하고 모델링하는 분야이다.
① 마케터가 최적의 Media Mix를 구성할 수 있도록 각 미디어(매체)별 최적 예산 할당 조합을 제안
② 도출된 최적 조합을 토대로 마케팅 효과가 얼마나 발생할 지 예측
-. 다시 말해, 마케터가 마케팅 캠페인을 계획(Planning)할 때 각 매체별로 얼마만큼의 비중을 할당할지에 대하여 제안하고 효과를 예측하는 방법론을 의미한다.
${(2)}$ 활용 데이터
-. 데이터는 다음과 같은 요소로 구성되어 있어야 한다. 전부 같은 기간 $t_{0}, \dots, t_{n}$에 대한 시계열 데이터여야 한다.
① KPI : 회귀모델의 Y에 해당. 성과에 해당한다. 예를 들면 판매량, 클릭수 등이 해당된다.
② 지출예산 : 회귀 모델의 X에 해당. 각 미디어별 지출한 예산 데이터
③ 외부요인 : 회귀 모델의 X에 해당. 날씨, 계절성, 경쟁사 성과 등 지출 예산 외에 KPI에 영향을 주는 인과관계를 갖는 데이터. 단, KPI와 지출예산 인과관계 사이에 끼어드는 데이터여선 안된다.
2) 베이지안 모델링과 최적화
${(1)}$ 이 논문을 이해하기 위해서는 두가지 학문적 배경을 이해하고 있어야한다. 베이지안 회귀와 순차 이차 최적화(SLSQP)가 그것이다.
-. 베이지안 회귀 : 회귀식의 파리미터를 베이지안 방법론을 이용하여 추정하는 회귀 방법론을 의미한다.
① MMM 문제를 풀고자 할 땐 파라미터에 대하여 비선형적인 회귀 문제를 풀어야하기 때문에 더이상 선형회귀에서 파라미터 추정에 사용하였던 최대우도추정법(maximizing the log likelihood)이나 최소제곱법(Minimizing the residual sum of squares)을 사용할 수 없다.
② 비선형적인 파라미터를 추정하기 위해 MCMC 방법론에 기반한 계층적 베이지안 방법론을 활용한다.
-. 순차 이차 최적화 : 이차 최적화(Quadratic Programming)에 뉴턴 방법론을 결합하여 순차적으로 최적화를 수행하는 방법론. 베이지안 모델 적합 후 미디어별 예산에 대한 최적해를 도출할 때 활용한다. - 본문
1) 광고 지출 효과에 대한 특성 및 모델링
-. Marketing Mix Models 문제를 제대로 풀기 위해선 다음의 이슈를 고려해야 한다.
①Carryover 효과 : 광고가 노출되서 나서 실제 KPI 실적으로 반영될때까진 다소의 시차가 필요하다. 회귀 모형에선 $y_{t}$와 $x_{t}$만의 선형관계를 t시점에 대해서만 고려하기 때문에, $t_{t-l}, ... t_{t-1}$시점의 과거 데이터를 현재 시점 t의 독립변수 $x_{t}$에 반영하기 위해선 특별한 처리가 필요하다.
②Shape 효과 : 광고 지출에 대한 실적을 모델링하기 위해서는 전통적인 선형회귀에서의 'X에 대한 Y의 선형(linear)' 가정은 타당하지 않다. 왜냐하면 광고비 지출에 대한 KPI 실적 반응은 경제학적인 한계체감성질을 갖고 있기 때문이다. 다시말해, 광고비를 무한정 집행한다고 해서 실적도 무한정 늘어나지 않는다. 이런 형태를 모델링하기 위한 비선형(non-linear)함수를 적용할 필요가 있다.
${(1)}$ Carryover 효과

adstock 함수의 예시. 검정색은 $w_{m}^{d}$에서 지연모수 $\theta_{m}$이 없는 경우, 빨간색은 존재하는 경우를 나타낸다.
L = lag의 값에 따라 가까울수록 1에 가까운 가중치를 가지고, 멀어질수록 그 가중치는 점차 낮아진다.
-. Carryover 효과를 모델링하기 하기 위해, 논문은 다음의 컨볼루션 함수를 제안한다.
$$adstock(X_{t-L+1,m},\dots,x_{t,m};w_{m},L) = \frac{\sum_{l=0}^{L-1}w_{m}(l)x_{t-l,m}}{\sum_{l=0}^{L-1}w_{m}(l)}$$ adstock 함수
(단, L은 효과를 고려할 시차, t는 컨볼루션을 적용하는 현재 시점, m은 미디어 매체)
-. 다시 말해, 현재 시점 t를 기준으로 크기 L인 Kernel(윈도우라고도 한다)을 움직이며 현재 시점 t의 값을 대치한다.
-. 이 때, $w_{m}$는 Geometric decay라고도 하는데, 아래와 같이 정의된다.
-. $w_{m}$은 윈도우 크기 L의 인덱스이자 시차인 l에 의존하므로, 현재 시점 t로부터 가까울수록 커지고 멀어질수록(= l이 커질수록) 점차 작은 값만을 반영하게 된다.$w_{m}(l;\alpha_m) = \alpha_{m}^{(l-\theta_{m})^{2}}$
단, $l = 0, \dots, L-1$, $0 < \alpha_{m} < 1, 0 < \theta_{m} \leq L-1$단,
① $\alpha_{m}$은 다음 시점 t + 1에 현재시점 t의 값을 얼마나 반영할것인지에 대한 retention rate
② l은 현재 시점부터 윈도우 크기 L...로 갈수록 점증하는 인덱스
③ $\theta_{m}$은 광고 효과가 최대화되는 지점을 모델링하기 위한 지연모수
-. 이 때, $\alpha_{m}$과 $\theta_{m}$은 베이지안 방법론으로 추정해야하는 파라미터가 된다.
${(2)}$ Shape 효과
-. 광고비 지출에 대한 효과를 효과적으로 모델링하기 위해서는, 효과(KPI)에 대한 지출(Spend)의 한계체감곡선을 효과적으로 모델링할 수 있는 곡률함수(Curvature Function)가 필요하다.
-. 저자들은 이 Shape효과를 모델링하기 위한 함수중 하나로 생물학에서 분자간에 결합을 모델링하는 함수인 Hill 함수를 제안하는데, 다음의 형태를 갖고 있는 함수이다.
Shape 효과를 모델링하는 Hill Function의 예시
파라미터에 따라 곡률의 모양이 변화한다.
$$Hill(x_{t,m};K_{m},S_{m}) = \frac{1}{1 + (x_{t,m}/K_{m})^{-S_{m}}}$$ 원본 Hill 함수
(단, t는 컨볼루션을 적용하는 현재 시점, m은 미디어 매체)
$K_{m}, S_{m}$은 추정해야할 파라미터가 된다.
-. 다만, 원본 Hill함수를 바로 모델에 적용하기엔 어렵다. 마케팅 분야의 경우 각 미디어 매체별로 도달할 수 있는 '최대 효과'가 다르기 때문이다. 이를 반영하기 위해 Hill함수를 변형한 $\beta Hill$ 함수를 제안한다.
$$\beta_{m} Hill_{m}(X_{t,m}) = \beta_{m} - \frac{K_{m}^{S_{m}}\beta_{m}}{x_{t,m}^{S_{m}} + K_{m}^{S_{m}}}$$ $\beta Hill$ 함수
(단, t는 컨볼루션을 적용하는 현재 시점, m은 미디어 매체)
$K_{m}, S_{m}$은 추정해야할 파라미터가 되고,
$\beta_{m}$은 뒤에서 살펴볼 회귀식의 파라미터로, 마찬가지로 추정해야할 파라미터이다.
2) 회귀식 결합
${(1)}$ Carryover Function과 Hill 함수의 결합
-. 앞서 살펴본 두 개의 함수를 다음의 항과 같이 결합한다.
-. 즉, $\beta Hill$ 함수 내부에 adstock 함수를 거쳐 전처리된 $x_{t,m}$이 들어가는 형태이다.$$x^{*}_{t,m} = adstock(X_{t-L+1,m},\dots,x_{t,m};w_{m},L)$$
$$\beta_{m}Hill( x^{*}_{t,m};K_{m},S_{m})$$
${(2)}$ (베이지안) 회귀식의 정의
-. $\beta_{m}Hill( x^{*}_{t,m};K_{m},S_{m})$을 이용하여 다음과 같이 성과(KPI)에 대한 회귀식을 정의한다.
$$y_{t} = \Gamma + \sum_{m=1}^{M}\beta_{m}Hill( x^{*}_{t,m};K_{m},S_{m}) + \sum_{c=1}^{C}\gamma_{c}Z_{t,c}+\epsilon_{t}$$
-. 각 항의 의미를 정리하면 아래 표와 같다.
항 설명 비고 $y_{t}$ t 시점의 성과(KPI)에 해당 $\Gamma$ 절편. 일종의 KPI 베이스라인에 해당한다. $\sum_{c=1}^{C}\gamma_{c}Z_{t,c}$ 지출 $x_{t,m}$이외의 요인은
외부변수 $Z_{t,c}$가 파라미터 $\gamma_{c}$로
선형결합$Z_{t,c}$는 외부변수의 샘플값
$\gamma_{c}$는 회귀식의 파라미터
또, $Z_{t,c}$는 $x_{t,m}$과 y 사이의 인과관계를 방해하지 않는
독립적인 변수여야함$\epsilon_{t}$ 잔차(Error) 회귀분석의 잔차 성질을 만족
즉 N(0,$\sigma$)를 따르는 WhiteNoise이며 변수들과는 독립
-. 다만, 실제 코드상에서 구현된 수식은 논문의 수식과는 다소 차이가 있다.
$$y_{t} = \Gamma + \beta_{trend} \cdot t^{expotrend} + season_{t} + \sum_{m=1}^{M}\beta_{m}F(x_{t,m}) + \sum_{c=1}^{C}\gamma_{c}Z_{t,c}+\epsilon_{t}$$
-. 실제 코드에서 구현된 각 항의 의미는 다음과 같다.
항 설명 비고 $y_{t}$ t 시점의 성과(KPI)에 해당 $\Gamma$ 절편. 일종의 KPI 베이스라인에 해당한다 $\beta_{trend}\cdot t^{expotrend}$ 시점 t의 시계열적 트렌드를 반영 $\beta_{trend}$와 $expotrend$는
추정해야할 파라미터$season_{t}$ $\sum_{k=1}^{t}[\gamma_{1,k}cos(\frac{2\pi k}{s}) + \gamma_{2,k}sin(\frac{2\pi k}{s})]$
으로 표현되는 계절성 모델링 항$\sum_{m=1}^{M}\beta_{m}F(x_{t,m})$ 컨볼루션 함수 ${F(x_{t,m})$을 포함하는
회귀항$\sum_{m=1}^{M}\beta_{m}Hill( x^{*}_{t,m};K_{m},S_{m})$에서
Hill 함수뿐만 아니라
다른 컨볼루션 함수도 활용 가능하도록 일반화$\sum_{c=1}^{C}\gamma_{c}Z_{t,c}+\epsilon_{t}$ 지출 $x_{t,m}$이외의 요인은
외부변수 $Z_{t,c}$가 파라미터 $\gamma_{c}$로
선형결합$Z_{t,c}$는 외부변수의 샘플값
$\gamma_{c}$는 회귀식의 파라미터
또, $Z_{t,c}$는 $x_{t,m}$과 y 사이의 인과관계를 방해하지 않는
독립적인 변수여야함$\epsilon_{t}$ 잔차(Error) 회귀분석의 잔차 성질을 만족
즉 N(0,$\sigma$)를 따르는 WhiteNoise이며 변수들과는 독립
3) 베이지안 최적화
${(1)}$ 베이지안 최적화를 활용하는 이유
-. 위에서 정의한 회귀모형식에서 추정해야할 모수는 다음과 같다.
-. 즉, 선형 회귀모델의 파라미터를 추정할때 활용하는 다음의 방법론은 활용하기 어렵다모수 선형 회귀 방법론 기반 추정 가능여부 이유 컨볼루션 $F(x_{t,m})$의 모수 불가능 추정해야할 파라미터가
선형성을 띄지 않음expotrend 불가능 추정해야할 파라미터가
비선형적인 t의 지수에 위치$\beta_{trend}$, $\beta_{m}$, $\gamma_{c}$ 가능 선형적으로 결합되어 있음
① 최대우도추정(MLE)법 : 모수에 대하여 닫힌 형태로 나타나지 않을 확률이 크다
② 최소자승법(OLS) : 파라미터에 대하여 선형결합이 아니기 때문에 활용할 수 없다.
-. Carryover 효과와 Shape 효과를 고려하기 위하여 도입한 항이 파라미터에 대하 비선형적이 될수밖에 없게 만들었고, 비선형 파라미터를 추정하기 위해서는 알고리즘적 방법론을 고민해야 한다.
-. 그 방법론 중 하나로 계층적 베이지안을 고려해볼 수 있다.
-. 한편으로, 베이지안 방법론을 채택하는 경우 연구자의 사전 믿음을 사전 모수(Prior Parameter)의 형태로 모델에 반영할 수 있다는 장점도 존재한다.
${(2)}$ 베이지안 추론 방법론
-. 이제, 목적은 앞서 정의한 회귀모델식의 파라미터를 베이지안 방법론을 이용하여 최적값을 추론하는 것이다.
-. 만약 데이터 우도함수의 분포와 사전분포가 '켤레 관계'를 맺고 있는 경우, 사후분포도 사전분포와 동일한 분포에 속하기 때문에 사후 분포의 종류를 쉽게 추정할 수 있고, 이를 이용하여 베이지안 추론식을 추정하기가 상대적으로 수월하다. 그러나, 현실의 많은 문제에서 이런 이상적인 관계일 확률은 매우 희박하다.
-. 사전분포가 우도함수(분포)에 대하여 켤레사전분포가 아니라서 발생하는 문제 중 하나는 사후분포를 명확하기 알기 어렵다는 것이다.
-.보통 베이지안 추론식에서 분모에 정의되는 적분식 $g_{1} = \int_{-\infty}^{\infty} h(\theta)L(y|\theta)d\theta$을 계산하기가 매우 까다롭고, 사후분포의 pdf가 닫힌형태로 정의되지 않는 경우가 매우 많다.
-. 베이지안 추론을 현실화하기 위해서는 적분식을 직접 계산하는 기존의 방법론이 아닌, 해석적 $\cdot$ 알고리즘적 방법론을 강구할 수 밖에 없었다.
-. 고민끝에 도출된 방법론 중 하나가 바로 몬테카를로 방법과 마코프 체인을 결합한 알고리즘인 Markov Chain Monte Carlo(MCMC) 이다. MCMC에 대한 간력한 설명은 아래와 같다.(
-. 물론, 실제 lightweightmmm은 Metropolis-hastings에서 Metropolis항만 따와 물리학의 '해밀토니안' 개념을 접목시킨 HMC에서, 한번 더 발전시킨 NUTS(No U-Turn Sampler)를 활용한다. 다만, mcmc에 대한 기본 개념은 크던 작던 위의 metropolis-hastings를 접목하여 활용한다.(HMC도 MH의 상태 전이 방법론을 활용한다)$$p(\theta | x) \propto p(x|\theta)p(\theta)$$
에서 시작하자. 우리의 목표는 사후분포 $p(\theta | x)$를 근사하는 것이다.
$p(\theta | x) = C \cdot p(x|\theta)p(\theta) \propto p(X|\theta)$ 의 관계가 성립된다.
이 때, C는 우리가 모르는 어떤 정규화 상수이다.(그리고 적분식 $g_{1}$과 연관되어 있어 구하기가 어렵다)
다시 말해, 정규화 상수 C를 알수있다면 명확한 등식관계로 추론식을 세울 수 있으나,
$g_{1}$을 알기 어렵기 때문에 보통은 쉽지 않다.① Stationary Distribution
$g_{1}$을 추정하기 어렵다면, 다른 방법을 통해서라도 사후분포 $p(\theta)$를 근사해야 한다.
이 때 Markov Chain Monte Carlo를 활용할 수 있다.
Markov Chain은 상태전이 확률(Transition Probability)이란게 존재한다.
상태전이확률은, 하나의 장에서 다음 장으로 전이될 때 이 장이 어떤 상태를 가질 것인지에 대한
확률을 의미한다.
다음의 상태전이확률이 존재한다고 하자
$$k(\alpha, \beta) = p(X_{n+1} = \beta | X_{n} = \alpha)$$
다시말해 이는 현재 상태 $\alpha$에서 다음 상태가 $\beta$로 전이할 확률을 의미한다.
가역성이 존재한다는것은 다음의 등식조건을 성립하도록 하는 확률분포 $\gamma(\alpha)$가 존재한다는 것이다.
$$k(\alpha, \beta)\gamma(\alpha) = k(\beta, \alpha)\gamma(\beta)$$
이런 식으로, 상태전이 상태가 등식이라면 시스템은 안정적인(Stationary) 상태가 되며,
다른 상태로의 전이는 더이상 이루어지지 않을 것이다.
(가장 이상적인 상태이다)
이 '안정적인(Stationary)' 상태 하에서 이 시스템의 궁극적인 '분포'는 다음과 같이 구할 수 있다.
양변이 같은 등식이라고 했으므로, 양변에 적분을 취하면
$\int_{\beta \in E} k(\alpha, \beta)\gamma(\alpha) d\beta = \int_{\beta \in E} k(\beta, \alpha)\gamma(\beta) d\beta = \gamma(\alpha)$
다시 말해, 이 분포는 Stationary할 때 $\gamma(\alpha)$를 가진다.② Detailed Balance
만약, 우리가 모사를 원하는 목적 분포를 $\gamma(\theta) = p(\theta)$라고 하고,
여기에 마코프 체인의 성격을 가미하여 $\theta$를 $\theta_{t-1}$과 $\theta_{t}$로 하자. 즉
$\alpha = \theta_{t}$, $\beta = \theta_{t-1}$과 같이 정할 수 있다.
<Reversible 할때의 MCMC 모식도>
$k(\theta_{t}|\theta_{t-1})$ 에서 어떤 무작위 샘플 $\theta_{t}$를 추출하고, 직전 체인에서 추출했던 $\theta_{t-1}$을 이용하여
$\frac{k(\theta_{t} | \theta_{t-1})\gamma(\theta_{t})}{k(\theta_{t-1} | \theta_{t} )\gamma(\theta_{t-1})} = \alpha$를
구할 수 있다.
그리고, 위에서 $\alpha = 1$일때 가장 이상적인 평형상태에 놓인다고 했으므로, 이 값으로 가는것을 목표로 한다.
문제는, $k(\theta)$는 임의로 추출한 어떤 표본값이므로, 이 값 아래에서
$\alpha = 1$에 도달하는 것이 매우 어려워진다는 것이다.
이를 보정하기 위해서 다음과 같은 미세조정항(Detailed Balance Term)을 추가한다.
$$\frac{\beta_{\theta^{t-1} \rightarrow \theta_{t}}}{\beta_{\theta^{t} \rightarrow \theta_{t-1}}}$$
이 때, 분모는 $\theta^{t-1}$에서 $\theta^{t}$로 전이될 확률, 분자는 $\theta^{t}$에서 $\theta^{t-1}$로 전이될 확률이다.
$\frac{k(\theta_{t} | \theta_{t-1})\gamma(\theta_{t}) \beta_{\theta^{t-1} \rightarrow \theta_{t}} }{k(\theta_{t-1} | \theta_{t} )\gamma(\theta_{t-1}) \beta_{\theta^{t} \rightarrow \theta_{t-1}}} = \alpha = 1$
여기서, 미세조정항을 우변으로 넘기도록 하자. 그러면
$\frac{k(\theta_{t} | \theta_{t-1})\gamma(\theta_{t})}{k(\theta_{t-1} | \theta_{t} )\gamma(\theta_{t-1})} = \frac{\beta_{\theta^{t} \rightarrow \theta_{t-1}}}{\beta_{\theta^{t-1} \rightarrow \theta_{t}}} = \alpha$③ 메트로폴리스 - 헤이스팅스 알고리즘
평형상태를 유지하기 위해 미세조정항을 추가한 결과, 각각의 전이확률의 비율인 확률 $\alpha$가 도출되었다.
$ \frac{\beta_{\theta^{t} \rightarrow \theta_{t-1}}}{\beta_{\theta^{t-1} \rightarrow \theta_{t}}} = \alpha$를
채택 - 기각 알고리즘과 연결짓자. 즉, 다음의 알고리즘을 따른다.
while t:
$\theta_{t} \leftarrow q(\theta_{t}|\theta_{t-1})$로부터 랜덤 추출한다.
$U \leftarrow Uniform(0,1)$로부터 랜덤 추출한다.
$\alpha = min[1, \frac{k(\theta_{t} | \theta_{t-1})\gamma(\theta_{t})}{k(\theta_{t-1} | \theta_{t} )\gamma(\theta_{t-1})} ]$를 계산한다.
if $\alpha < U$:
$\theta_{t}$를 폐기, $\theta_{t-1} \rightarrow \theta_{t}$
if $\alpha \geq U$:
$\theta_{t}$를 유지, $\theta_{t} \rightarrow \theta_{t}$
이 채택 - 기각 알고리즘을 동작시키면 총 반복 t에 대하여
$\theta = [\theta_{1}, \dots, \theta_{t}]$의 리스트가 도출되는데, 여기에 대한 평균(혹은 중앙값)을 구하면
베이지안 최적해를 구할 수 있고, 이것은 우리가 모사하기를 원했던 $P(\theta)$ 분포의 모수에 가까워진다.③ (Target Y를 고려한) 메트로폴리스 - 헤이스팅스 알고리즘
그러나, 우리가 관심이 있는건 $\theta_{t}$와 $\theta_{t-1}$의 전이가 아니다.
$\theta_{t}$와 $\theta_{t-1}$의 전이 확률이 Target Y에 대하여 평형상태를 이루길 원한다.
따라서, $k(\theta_{t} | \theta_{t-1})$와 $k(\theta_{t-1} | \theta_{t})$를 다음의 우도함수로 대체한다.
$k(\theta_{t} | \theta_{t-1}) \rightarrow L(Y | \theta_{t-1})$
$k(\theta_{t-1} | \theta_{t}) \rightarrow L(Y | \theta_{t})$
그럼 이제 메트로폴리스-헤이스팅스 알고리즘은 아래와 같이 수정된다
while t:
$\theta_{t} \leftarrow q(\theta_{t}|\theta_{t-1})$로부터 랜덤 추출한다.
$U \leftarrow Uniform(0,1)$로부터 랜덤 추출한다.
$\alpha = min[1,\frac{L(Y | \theta_{t-1})\gamma(\theta_{t})}{L(Y | \theta_{t})\gamma(\theta_{t-1})}]$를 계산한다.
if $\alpha < U$:
$\theta_{t}$를 폐기, $\theta_{t-1} \rightarrow \theta_{t}$
if $\alpha \geq U$:
$\theta_{t}$를 유지, $\theta_{t} \rightarrow \theta_{t}$
이 때, 우도함수는 $\theta$를 모수로 취했을 때 Y값에 대한 우도를 도출하는 함수(dnorm 함수 등)을 활용한다.
-. HMC와 MCMC에 대한 내용은 추후에 더 자세하게 다루고자 한다.
4) 모델 결과 표출 및 미디어 믹스 최적화
-. 위에서 적합한 베이지안 회귀 모델식을 이용하여, 마케팅 실무에서 크게 관심을 가질만한 두 가지 문제에 대한 해답을 얻을 수 있다.
-. 하나는 ROAS(또는 mROAS)이고, 또 하나는 KPI를 최대화하는 최적의 예산 믹스를 역으로 도출하는 미디어 예산 최적화(Media Budget Allocation Optimization)이다.
${(1)}$ ROAS and mROAS
-. ROAS(Return on ad spend)은 광고비 집행(Spend) 1단위당 얻은 KPI(return)을 의미한다. 즉, 마케팅 성과 측정의 지표이다.
-. ROAS를 측정하고자 할 때는 전체 시계열 데이터를 다음의 세 기간으로 분리해야한다.
① 전환 기간(Change Period) : 성과를 측정하고자 하는 대상 기간
② 전환 전 기간(Pre-change period) : 마케팅 예산이 집행되고 직후의 일정 기간. 마케팅 전략이 성과를 거두기 위해서는 어느정도의 시간이 필요하기 때문에 이 기간은 아직 성과가 창출되지 않은 준비기간으로 간주한다
③ 전환 후 기간(Post-chane period) : 전환 기간 이후 데이터가 존재하는 지점까지의 기간. 보통은 전환 전 기간과 동일한 길이를 전환 후 기간으로 설정한다.
-. ROAS는 아래와 같은 방법으로 계산한다.
-. 복잡한 파라미터들이 여럿 들어가있어 어려워 보이지만, 이 식이 가리키는 기본 개념은 굉장히 심플하다.$ROAS_{m} = \frac{\sum_{t_{0} \leq t \leq t_{1}+L-1} \widehat{Y_{t}^{m}}(x_{t-L+1, m}, \dots, x_{t,m}; 1 \leq m \leq M ; \Omega) - \widehat{Y_{t}^{m}}(\tilde{x}_{t-L+1, m}, \dots, \tilde{x}_{t,m}; 1 \leq m \leq M ; \Omega)}{\sum_{t_{0} \leq t \leq t_{1}}x_{t,m}}$ 단,
① $t_{0}$는 전환 기간(Change Period)의 시작, $t_{1}$은 전환 기간의 끝
② L은 베이지안 모델 적합시에 사용한 윈도우 사이즈
③ M은 매체 종류
④ $\Omega$는 도출된 베이지안 회귀식(의 파라미터)
⑤ $\tilde{x}$는 pre-change와 post-change엔 광고비 x와 같으나, change period엔 0으로 처리한 변환된 광고비
① 실제 지출한 광고비에 대하여 예측 KPI를 구하고, 광고비를 단 한푼도 지출하지 않았다고 가정했을때의 KPI를 구해 둘 사이의 차이를 구하면 순수하게 광고의 집행이 KPI에 기여했다고 볼 수 있는 추가적인 이득이 나오게 된다.
② 이를 총 광고비 총합 $\sum_{t_{0} \leq t \leq t_{1}}x_{t,m}$로 나누어 정규화한다.
-. mROAS의 계산 : 한편, 제로 지출을 가정하여 ROAS를 계산해볼수 있지만, 현재 광고비 지출 수준에서 1단위 더 늘렸을때의 (기대되는) KPI 수익도 구해볼수 있다. 이를 mROAS라고 하고, 아래와 같이 계산한다.$mROAS_{m} = \frac{\sum_{t_{0} \leq t \leq t_{1}+L-1} \widehat{Y_{t}^{m}}(\tilde{\tilde{x}} _{t-L+1, m}, \dots, \tilde{\tilde{x}}_{t,m}; 1 \leq m \leq M ; \Omega) - \widehat{Y_{t}^{m}}(x_{t-L+1, m}, \dots, x_{t,m}; 1 \leq m \leq M ; \Omega)}{(증가율) X \sum_{t_{0} \leq t \leq t_{1}}x_{t,m}}$ 단,
① $t_{0}$는 전환 기간(Change Period)의 시작, $t_{1}$은 전환 기간의 끝
② L은 베이지안 모델 적합시에 사용한 윈도우 사이즈
③ M은 매체 종류
④ $\Omega$는 도출된 베이지안 회귀식(의 파라미터)
⑤ $\tilde{\tilde{x}}$는 pre-change와 post-change엔 광고비 x와 같으나,
change period엔 x에 증가율(ex. 1 + 0.01)을 곱하여 증액한 변환된 광고비
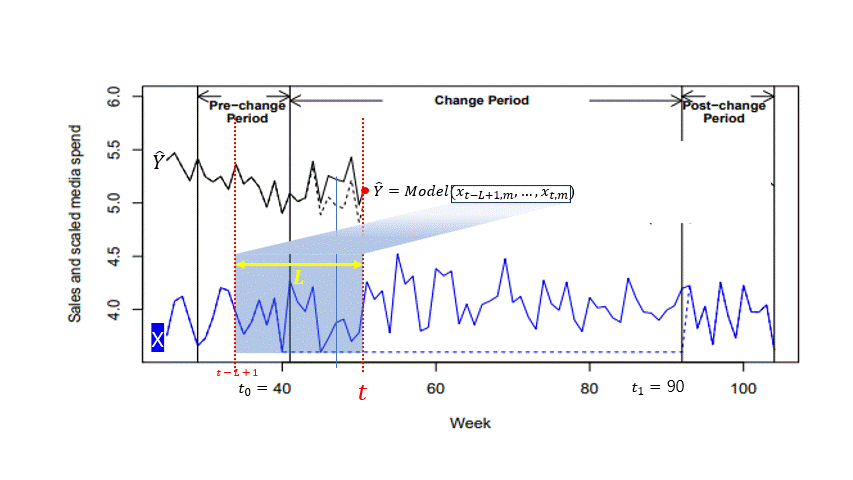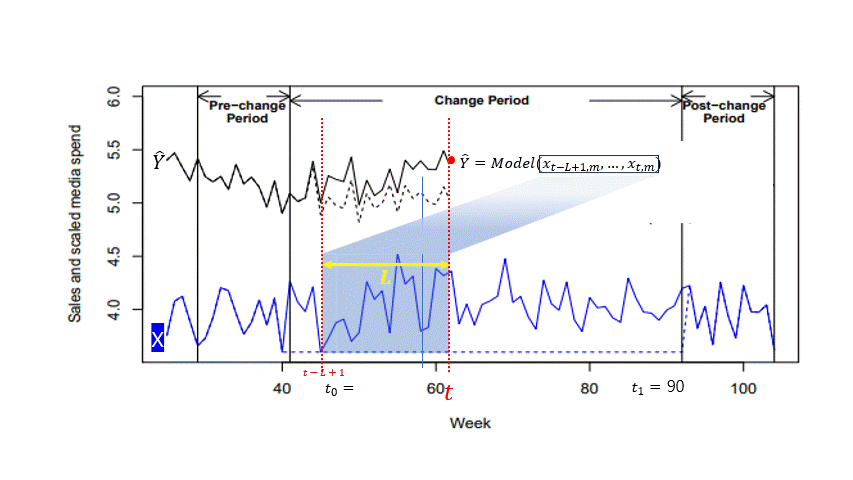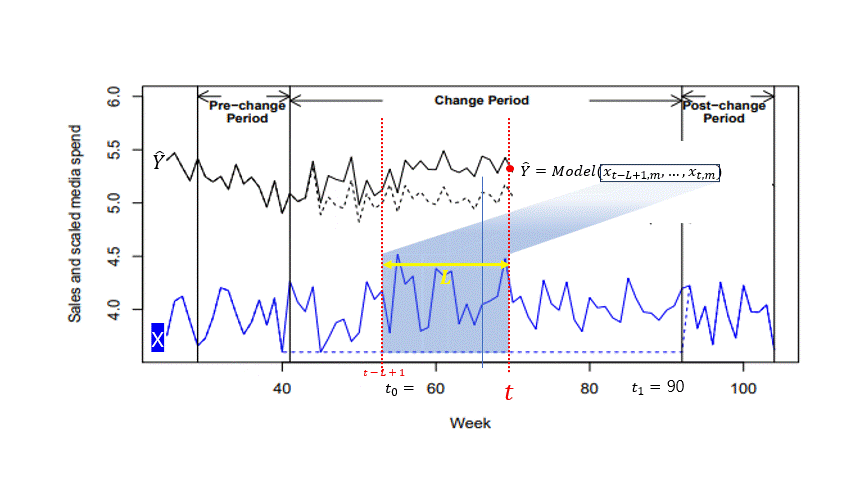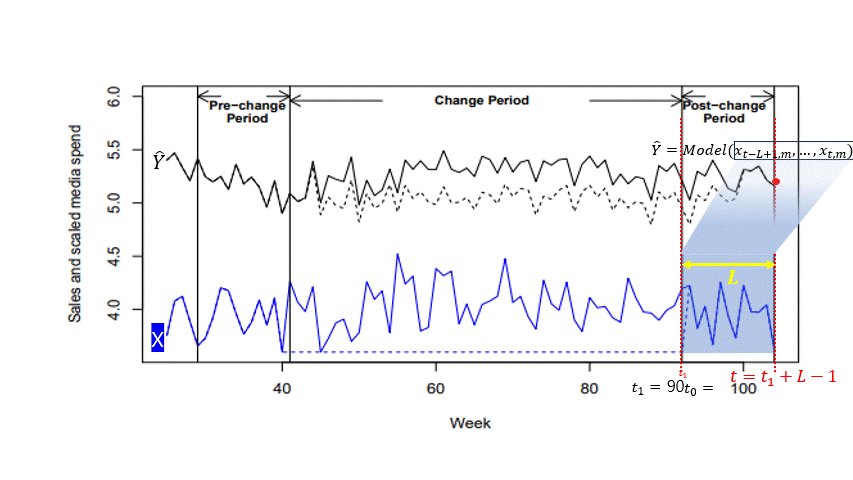
ROAS 계산 및 최적 예산 믹스에 활용되는 $\sum_{t_{0} \leq t \leq t_{1}+L-1} \widehat{Y_{t}}$의 동작 예시
크기 L의 윈도우를 $t_{0}$부터 시작하여 $t_{1} + L - 1$까지 움직이며 $\widehat{Y_{t}}$를 생산한다.
그리고, 이 구간내에서 생산한 예측값 $\widehat{Y_{t}}$를 모두 더한 값을 최대화 하는것을 Optimization의 목적으로 한다.
${(2)}$ 미디어 믹스 최적화
-. Marketing Mix Modeling의 또다른 관심사는 'KPI를 최대화할 수 있는 각 마케팅 믹스별 지출 X는 무엇인가' 일 것이다.
-. 보통 마케팅 현업에서 한 가지 매체에만 광고를 집행하는 경우는 굉장히 드물다. 여러개의 채널을 한대 섞어야(Mix) KPI가 극대화되기 때문에, 보통 마케터들은 여러개의 매체를 혼합하여 하나의 캠페인을 구성하는 쪽을 선호한다.
-. 그러나 캠페인을 수행할 때는 현실적인 예산 한도라는것이 존재한다. 가령 이 총액을 C라고 가정하자. 제약조건이 C 아래에서 각 미디어별로 예산을 집행할 때, KPI가 최대화 되는 최적의 미디어 예산 믹스 $X_{0}$를 도출하는것이 Media Budget Allocation의 목적이 된다.
-. 이를 위하여 볼록함수 최적화(Convex Optimization)기법 중 이차식에 대한 문제를 푸는 Quadratic Programming 알고리즘을 활용하여 최적해 $X_{0}$를 도출한다.
-. 최적화를 수행하기 위해서는 최적화의 목적이 되는 목적식과, 최적화를 수행할 때 최적해의 공간을 제약하는 제약식 두 가지가 정의되어야 한다.
-. 이 때, 베이지안 추론에서 도출되는 $\Omega$의 특성을 이용하여 목적식을 살짝 변경할 수 있다.목적식 : Maximize $\sum_{t_{0} \leq t \leq t_{1}+L-1} \widehat{Y_{t}}(x_{t-L+1, m}, \dots, x_{t,m}; 1 \leq m \leq M ; \Omega)$
제약식 : Subject to $\sum_{t_{0} \leq t \leq t_{1}+L-1} \sum_{1 \leq m \leq M} x_{t,m} = C$단,
① $t_{0}$는 전환 기간의 시작, $t_{1}$은 전환 기간의 끝
② L은 베이지안 모델 적합시에 사용한 윈도우 사이즈
③ M은 매체 종류
④ $\Omega$는 도출된 베이지안 회귀식(의 파라미터)
⑤ C는 총 예산 제한
-. MCMC 최적화 과정에서, 각각의 파라미터 $\theta_{1}, \dots, \theta_{n}$가 있다고 가정하자. 예를 들면 위에서 설명한 $\beta_{trend}$, $\beta_{m}$, $\gamma_{c}$ 같은 것들이다.
-. 이 각각의 파라미터들이 최적화 Iteration $iter_{1}, \dots, iter_{j}$을 거치며 j개의 파라미터 상수를 흔적같이 저장하게 된다.
-. 보통 베이지안 추론에서 최적의 베이지안 추정해는 $iter_{1}, \dots, iter_{j}$의 평균이나 중앙값등을 활용하지만, 이를 확장하여 목적식 자체에 대한 최적의 추정해를 구할수도 있다. 단순하게, j개의 파라미터를 거쳐 도출한 예측값 $\widehat{Y_{t}}$에 대한 평균을 구한다.
-. 또는, 최적화 자체를 J번 수행하여 J개의 최적해 $X_{0}, \dots, X_{j}$를 도출하고, 그 최적해의 리스트 $[X_{0}, \dots, X_{j}]$의 평균, 중앙값을 통해 베이지안 최적해를 구하고, j개의 샘플들을 활용하여 베이지안 신용구간을 구할수 있도록 하는 방법도 있다.Maximize $ \frac{1}{J} \sum_{1 \leq j \leq J}\sum_{t_{0} \leq t \leq t_{1}+L-1} \widehat{Y_{t}}(x_{t-L+1, m}, \dots, x_{t,m}; 1 \leq m \leq M ; \Omega_{j})$
Subject to $\sum_{t_{0} \leq t \leq t_{1}+L-1} \sum_{1 \leq m \leq M} x_{t,m} = C$목적식 수정버전 1
각 파라미터의 의미는 상동
J는 MCMC의 총 반복횟수(Iteration)
-. 최적화를 거쳐서 도출된 최적해 $X^{m}$을 매체 m에 대한 최적 광고비라 하며, 이는 제한조건 C 하에서 KPI를 최대화하는 최적의 광고비 X값이 된다.Maximize(j) $ \sum_{1 \leq j \leq J}\sum_{t_{0} \leq t \leq t_{1}+L-1} \widehat{Y_{t}}(x_{t-L+1, m}, \dots, x_{t,m}; 1 \leq m \leq M ; \Omega_{j})$
Subject to $\sum_{t_{0} \leq t \leq t_{1}+L-1} \sum_{1 \leq m \leq M} x_{t,m} = C$목적식 수정버전 2
각 파라미터의 의미는 상동
J는 MCMC의 총 반복횟수(Iteration)
위 과정을 통해 도출된 최적해 리스트 $[X_{0}, \dots, X_{j}]$의 평균, 중앙값등을 구해 베이지안 최적해 구하기를 적용한다.
이 방법은 베이지안 신용구간을 구하는데 활용할 수 있어 특히 유용하다.
-. lightweightmmm은 Convex Optimization을 수행할 때 Scipy의 순차 이차 최적화(SLSQP)를 활용한다.
-. 실제 코드상에는 다음과 같이 구현되어 있다.
-. 위와 같이 구현되어 있기 때문에, 한가지 특이사항이 발생한다.
< 최적화(optimize_media) 모듈의 구조도 요약>
<generate_starting_values>
초깃값을 생성하는 함수로, Objective Function에 초깃값 $x_{0}$를 공급하여 최초의 kpi Y를 생성하도록 한다.
다음의 과정을 거쳐 최초값을 생성한다.
① 미디어 데이터별 평균화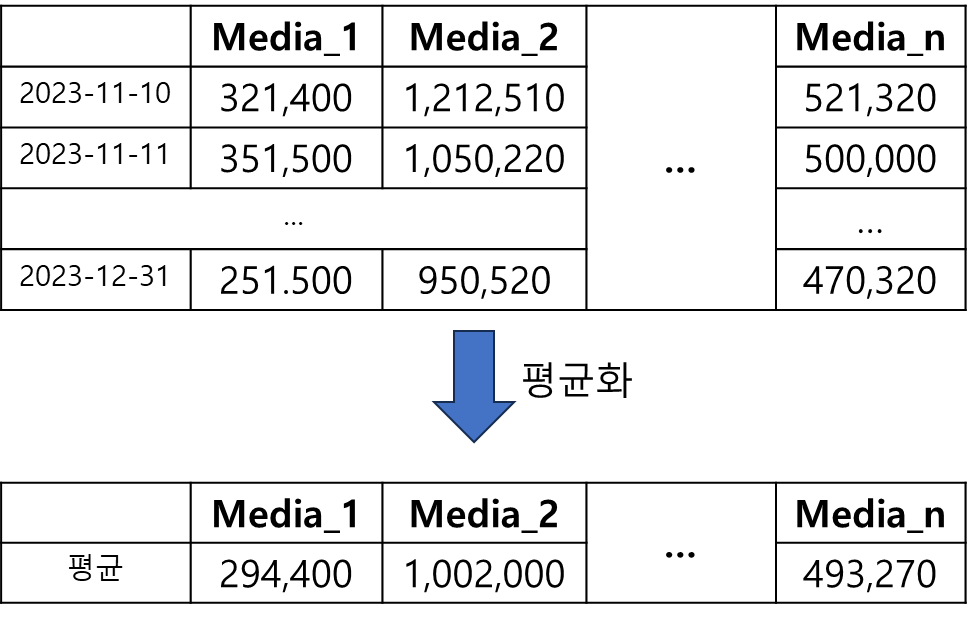
각 미디어 집행 데이터별로 기간의 평균값을 구한다.
평균값을 구하는 데이터는 베이지안 모델 학습시에 모델에 저장된 Train 데이터(mmm.media)가 활용된다.
평균값은 각 단위(즉, 여기서는 일자)를 기준으로 구했기 때문에, 이는 각 미디어의 단위 기댓값(즉, 일별 단위값)이 된다.
② n_time_periods 곱해 기간 기댓값으로 변환
① 에서 구한 값은 단위 기댓값이었기 때문에, 이를 원하는 기간 기댓값으로 변환한다.
방법론은 그냥 간단하게 '우리가 원하는 최적화 기간(=n_time_period)를 곱해 구한다.
③ 총합값으로 나누어 비율화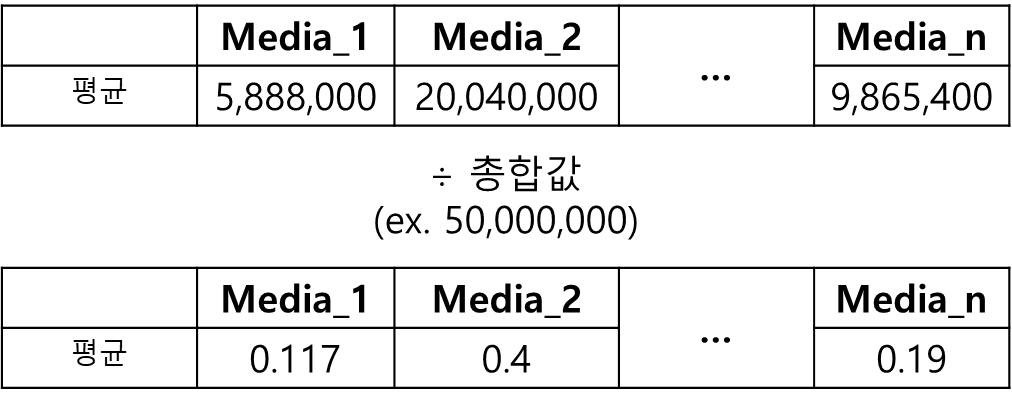
각 미디어 매체별 평균값을 총합값으로 나누면, 총합이 1인 비율로 바뀐다.
④ 총 예산제한(Budget)을 곱해 나눠먹기
총 예산제한값을 비율별로 곱하면, 각 미디어별로 기대되는 예산 최적 분배값의 초깃값을 도출할 수 있다.
이것을 초기값 $x_{0}$로 할당하여 최적화를 시작한다.<get_lower_and_upper_bound>
미디어 데이터의 평균값 ( <generate_starting_values>의 평균화 참조 )을 기준으로
상한과 하한의 구간을 정의
구체적으로는 각 미디어별로 평균화를 수행한 후, n_time_periods를 곱하여 기간 기댓값으로 변환한다.
기간 기댓값에(상한%, 하한%)를 곱한 값을 각각 상한값과 하한값으로 결정하며, 그 %는 하이퍼 파라미터로 결정할 수 있다.
(기본값은 20%)<objective_function>
최적화시 목적이 되는 y값을 각 Iteration별로 생산하는 함수. 즉 최적화의 목적함수이다.
다음의 과정을 거쳐 KPI y값을 생산한다.
① Prediction용 데이터 Shape 정의
(n_time_periods, 미디어 매체 개수)로 Shape를 정의한다.'
② $x_{i}$ 입력
최초 시작이라면 <generate_starting_values>에서 생산된 최초값을,
도중이라면 i번째 Iteration의 x값 $x_{i}$를 입력받는다.
③ Prediction용 데이터로 변환
$x_{i}$를 n_time_periods로 나누어 기간 기댓값을 단위(일별) 기댓값으로 다시 되돌리고,
1개 행의 벡터에 불과한 이 데이터를 n_time_periods만큼 반복하여 붙여
( n_time_periods, 미디어 매체 갯수)의 행렬로 확장한다.
④ 적합한 베이지안 회귀식에 Prediction용 데이터 투입
( n_time_periods, 미디어 매체 갯수)인 위 Prediction용 데이터를 모델에 투입하여 KPI를 산출
각 미디어 매체(열)별로 평균화를 수행하고, 총합한 값을 목적함수의 값(=KPI y)로 산출하여 최적화기에 전달<Budget_constraint>
$이번 iteration의 최적화 결과값 x_{i}$를 총합한 값과 총 예산 제약(Budget)간 차이를 구해 최적화기에 전달, 즉
$$(\sum_{m=1}^{M} x_{i,m}) - Budget$$
최적화기는 위 값이 0이 되도록(즉, $\sum_{m=1}^{M} x_{i,m} = Budget$) 제약조건 하에 최적화를 수행하게됨
① 총 예산 제약(Budget)은 상한과 하한(get_lower_bound_and_upper_bound)내에 있어야 한다. 만약, 총 예산제약을 5천만원으로 결정했는데, 상한과 하한이 각각 3천만원과 2천만원이라면 최적화는 당연히 실패할것이다.(예산 제약이 상한과 하한 내에 존재하지 않는경우 ("Budget given is larger than the upper/lower bounds" 경고를 띄운다)
② 문제는, 상한과 하한은 미디어 데이터의 평균값이라는 이미 결정된(즉, Historical한) 데이터를 기반으로 계산하기 때문에 변화를 줄 수 있는 여지가 상당히 제약된다는 점이다.
③ 사용자가 상한과 하한을 조절할 수 있는 방법은 (상한%, 하한%)를 조절하거나, 혹은 n_time_periods를 늘리는 방법밖에는 없다. 각각이 주어졌을때의 Bound는 아래와 같은 식으로 계산할 수 있다.
$$평균값 = \sum_{t=1}^{T} \sum_{m=1}^{M} MediaData_{t,m} * n\_time\_periods$$
$하한 = 평균값 * (1-하한\%)$
$상한 = 평균 * (1+상한\%)$
'논문 Review' 카테고리의 다른 글
| High-Resolution Image Synthesis with Latent Diffusion Models (0) | 2024.03.16 |
|---|---|
| 트랜스포머 알고리즘의 등장 : Attention is all you need (0) | 2023.05.23 |
| 논문 Review : SR-CNN(Spectral Residual Convolution Neural Network) (4) | 2023.05.11 |


