Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- bayesian
- 미적분 #평균값 정리 #로피탈의 정리 #접선의 방정식
- Marketing Mix Modeling
- 프로그래머를 위한 선형대수 #선형대수 #LU분해
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #야코비 회전법 #QR법 #하우스홀더반사 #행렬회전
- 수리통계
- 프로그래머를 위한 선형대수 #선형대수 #고유분해 #고윳값 #고유벡터
- lightweightmmm
- 프로그래머를 위한 선형대수 #선형대수 #행렬계산
- bayesian inference
- 시계열분석 #Time-Series Analysis #이상탐지 #Anomaly Detection #Spectral Residual #CNN #SR-CNN
- Media Mix Modeling
- 미적분
- Optimization
- 미적분 #사인과 코사인의 도함수
- mmm
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #고유분해
- 미적분 #접선의 방정식 #최적화 #뉴턴법 #뉴턴-랩슨법
Archives
- Today
- Total
문과생 네버랜드의 데이터 창고
High-Resolution Image Synthesis with Latent Diffusion Models 본문
*20240708 수정 : 목적함수 도출 부분에서 설명이 부실했던 부분을 보강하였습니다
<요약>
- Diffusion은 어떤 유의미한 패턴(ex. 뭉쳐있는 가루 입자)에서 점차 랜덤한 가우시안 노이즈(ex. 용해된 가루 입자)로 확산하는 분자들의 움직임 의미하는 물리학 개념이다
1) 각각의 분자는 각각 랜덤한 가우시안 노이즈 $N(0,I)$ 를 따라 무작위적인 운동을 수행하고, 결국엔 패턴이 무작위한 임의의 위치로 확산(Diffusion)하게 된다.
2) 만약, 패턴이 있는 상태에서 무작위한 상태로 확산한 경로(=함수)를 모델링 할 수 있다면, 역으로 무작위한 상태에서 패턴이 있는 상태로 되돌리는 것도 가능할 것이다.
입자의 확산(Forward Diffusion)은 물리학적인 개념이다.
3) 이 때, 패턴이 있는 상태에서 무작위 상태로 확산하는 과정을 Forward DIffusion, 무작위 상태에서 패턴이 있는 상태로 되돌리는 과정을 Reverse Diffusion이라고 지칭한다.
4) 이 중 Reverse Diffusion 과정의 학습은 Diffusion 계열 모델의 핵심 기능으로서,
① 변분 추론(Variational Inference) 테크닉인 ELBO를 구하는 방법을 이용하여 손실함수(Loss Function)을 도출하고,
②이를 유한 차시(Finite time) 마코프 체인을 통해 무작위 상태에서 다시 패턴이 있는 상태로 되돌리는 신경망(Neural Network) Denoiser를 학습시키는것을 목적으로 한다.(Jonathan, Ajay and Pieter, 2020)
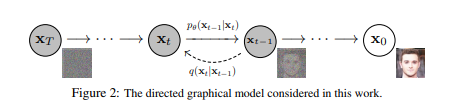
Diffusion Process의 예시.
우리의 목적은 $X_{T},...,X_{0}$의 유한 차시 마코프 체인을 통해
$N(0,I)$를 따르는 무작위 가우시안 노이즈($X_{T}$)에서 패턴이 있는 원본 이미지($X_{0})$를 복원하는
확률 함수 $P_{\theta}(X_{t-1}|X_{t})$를 대리하는 Denoiser Neural Network를 학습하는 것이다. - Latent Diffusion은 위에서 설명한 기본적인 Diffusion 모델에 다음의 두 가지 기능을 덧붙여 장점을 극대화한 모델이다.
1) 잠재 공간 압축 : Reverse Diffusion Process의 학습을 Auto Encoder를 이용하여 특징만 압축하여 추출한 잠재공간(=Latent Space)안에서 수행한다.
기존의 DIffusion Model들은 $X_{0}$로 대표되는 실제 이미지 복원이 목적이라면, Latent DIffusion은 Auto Encoder를 통해 압축된 잠재 공간에서의 특성 데이터 $Z_{0}$를 복원하는 것을 목적으로 한다.
2) Diffusion 조건 추가: 특정 조건하(ex. 텍스트 프롬프트, 이미지 등) 에서 Diffusion을 수행하도록 하는 매커니즘.
Denoiser Neural Network이 샘플링을 수행할 때, 원래의 Hidden State인 $Z_{t-1}$에 대하여 $Z_{t}$를 구하지 않는다.
대신 어떤 특정 조건을 결합한 $Z'_{t} = softmax(\frac{QK^{T}}{\sqrt{d}}) \cdot V$로 Reverse Diffusion을 수행한다. Transformer에 익숙한 사람들을 눈치챘겠지만, 이는 Self Scaled dot product attention과 동일하다.
<본문>
- 서론
1) 관련 연구(Related Work)
(1) 이미지 생성에서의 생성형 모델들의 역할은 GAN과 VAE로 대표된다.
(2) 최근에는 Diffusion Probablistic Model이 State-of-the-art한 성능들을 나타내며 주목받고 있다.
-. 이는 기본적으로 샘플링(스케쥴링) 기법의 발전, 계층적 접근방법의 등장에 힘입은 바가 크다.
(3) 각각의 이미지 생성 알고리즘들의 단점들을 보완하기 위해, 최근의 연구들은 2단계 이미지 생성을 이루어내는 방법으로 연구가 진행되고 있다
-. Text Embedding과 이미지의 결합 분포로부터 자기회귀적(AutoRegressive) 모델을 통해 원본 이미지 복원을 꾀하는 VQ-VAE나, 적대적 학습의 개념을 포함한 VQGAN은 뛰어난 성능을 보여줬다.
-. 그러나, 이들 모델은 기본적으로 수십억단위의 파라미터를 학습시켜야 하는 매우 비싼 학습 비용을 치뤄야 한다. - 본론
1) 방법론(Method)
(1) 결국, 저자들의 고민은 '어떻게 해야 학습 비용을 낮출 수 있을 것인가' 에서 부터 시작한다.
Latent Diffusion의 구조도
① 가장 왼쪽 빨간색 공간은 AutoEncoder에서 압축을 담당하는 Encoder($\varepsilon$)와 다시 원본 이미지로 복원하는 Decoder($D$)를 의미
② 초록색 Latent Space는 압축된 latent 공간에서 Diffusion Process를 수행하는 모습을 나타낸다.
이 중, 위쪽의 'Diffusion Process'는 실제 학습에선 활용하지 않는 가상의 Process이다.
실제 학습은 가우시안 노이즈 $Z_{T}$ ~$N(0,I)$에서 원본에서 가장 가까운 Latent $Z_{0}$로 복원하는
아래쪽 Reverse Diffusion만 활용한다.
③ 가장 오른쪽 핑크색 공간은 조건부 Cross-Attention 매커니즘을 수행하는 컨디셔너 $\Gamma_{\theta}$를 나타낸다. $\Gamma_{\theta}$는 요컨데 트랜스포머가 될 수 있으며, 투입된 Text Prompt(ex. Beautiful, School, AnimeGirl 등)를 토큰화 후 임베딩으로 변환하여 Denoiser Neural Network $\epsilon_{\theta}$에서 Cross Attention을 수행(QKV) 할 수 있도록 준비한다.
-. Jonathan, Ajay and Pieter, 2020 에서 수행한것과 마찬가지로 무의미한 손실 함수의 항들을 제거(To ignore perceptually irrelevant details by undersampling the coreesponding loss terms)함으로서 경령화를 꾀한다 해도 문제는 해결되지 않는다. 근본적으로, 고차원의 '픽셀 공간'에서 학습을 수행하는 것은 그 자체로도 굉장히 비싼 학습 비용을 치뤄야하는 문제가 있다.
-. 즉 문제는 손실함수의 경량화가 아니다. 학습이 출발하게 되는 '픽셀 공간'이라는 차원 자체가 너무나도 많은 정보를 내포하고 있는 고차원적 공간이라 어쩔 수 없는 비용 절감의 한계가 발생하게 된다.
(2) 그렇다면, 픽셀공간을 대신할만한, 필수 정보를 포함하고 있으면서도 필요 없는 디테일(perceptually irrelevant details)을 무시하는 압축된 공간을 대신 쓰면 학습 비용 문제를 해결할 수 있을 것이다.
(3) 이를 위해, 저자들은 원본 이미지를 잠재 공간으로 압축하는 아이디어를 도입하여, 학습을 두 단계로 분리한다.
-. 잠재공간 압축 : 원본 픽셀 공간에서 잠재 공간(Latent Space)으로 이미지 압축을 수행한다. AutoEncoder를 학습시키는데, RGB값을 갖는 픽셀 이미지 $x \in \mathbb{R}^{H\times W\times 3}$를 Encoder $z=\varepsilon(x)$는 다음의 Factor함수 f를 하이퍼 파라미터로 이용하여 압축한다.
이 때, AutoEncoder를 학습하는데 활용되는 손실함수는 Perceptual Loss와 Patch-based Adversarial Loss를 결합하여 사용한다.
빨간색 공간 AutoEncoder를 통해
잠재공간의 표현형 $Z_{0}$로 압축하는 구조의 표현도.
$z \in \mathbb{R}^{h\times w\times c}$ 라고 할 때
$f = H/h = W/w$
즉, 잠재 공간에서의 압축된 차원 h,w는 Factor 하이퍼 파라미터 f에 따라 결정된다.
또한, 저자들은 실험을 통해 다음의 지수함수가 최적의 f를 결정짓는다고 밝히고 있다.
$f = 2^{m}$
즉, 최종적으로 m이 바로 하이퍼파라미터가 된다.
-. Reverse Diffsuion Process 학습$L_{Autoencoder} = min_{\epsilon, D}max_{\psi}\begin{pmatrix}
L_{rec}\begin{bmatrix}x,D(\epsilon(x)) \end{bmatrix} - L_{adv}\begin{bmatrix}D(\epsilon(x)) \end{bmatrix} + logD_{\psi}(x)+L_{reg}\begin{bmatrix}x;\epsilon,D\end{bmatrix}
\end{pmatrix}$
이 때, $L_{rec}$은 재구성 오차, $L_{adv}$는 Adversial Loss, $D_{\psi}$ 는 판별자(Discriminator)의 Loss, $L_{reg}$는 정규화항을 의미한다.
논문에선 정규화항으로 KL-reg와 VQ-reg를 고려한다.
① 공간이 축소되면, 이제 축소된 잠재공간의 표현형 $z$를 이용하여 Reverse Diffusion Process를 학습하게 된다.
② 목적은 Denoiser로 사용된 U-Net $\eta_{\theta}$를 학습시키는 것인데, 구체적인 학습 방법은 Denoising Deffusion Probabilistic Model( Jonathan, Ajay and Pieter, 2020)에서 다룬 방법론을 채용한다.(이와 관련된 내용은 다음에 다루고자 한다) 우선, 손실함수는 다음과 같이 정의할 수 있다.
기본 개념 정의 논의에 앞서, 다음과 같이 개념들을 정의하고자 한다.
① $x_{T}$는 Forward Diffusion Process의 가장 끝단, 즉 랜덤 가우시안 노이즈라고 하자
$x_{t}$는t = 1.....T-1인 Forward Diffusion Process의 중간 과정이라고 하자.
$x_{0}$는 Forward Diffusion Process의 시작점, 즉 원본 이미지(에 가까운 Latent)라고 하자.
② $q(x_{1:T}|x_{0})$는 Forward Diffusion Process를 정의하는 함수이다.
-. 한편, $q(x_{t}|x_{t-1})$은 $x_{t-1}$에서 $x_{t}$로 한 단계 이동할 때의 중간과정을 다룬 함수이고, 가우시안 분포를 따른다.
$ q(x_{t}|x_{t-1}) := N(x_{t} | \alpha_{t}x_{t-1}, \sigma_{t}^{2}\mathbb{I})$
-. 중간 단계를 다룬 $q(x_{t}|x_{t-1})$ 를 이용하여 $q(x_{1:T}|x_{0})$ 를 정의하면 아래와 같이 도출할 수 있다.
$q(x_{1:T}|x_{0}) = \prod_{t=1}^{T} q(x_{t}|x_{t-1})$
-. 이 때, $x_{1:t}$라는 관심이 없는 중간과정을 없애고, $x_{0}$가 주어졌을 때 t시점의 $x_{t}$가 바로 주어질 확률을 구하면 논리 전개가 조금 더 편리할 것이다.
$q(x_{1:T}|x_{0})$를 AR(1) 의 개념을 응용하여 재귀적으로 구하면 다음과 같이 정의할 수 있다.
$q(x_{t}|x_{0}) = N(x_{t}|\alpha_{t}x_{0}, \sigma_{t}^{2}\mathbb{I})$
-. $q(x_{t}|x_{0})$를 이용하여 $x_{t}$를 다음과 같은 선형식으로 정의할 수 있다.
$x_{t} = \alpha_{t}x_{0} + \sigma_{t}\epsilon$
이 때 $\epsilon$은 $N(0,1)$을 따르는 랜덤 가우시안이다.
③ $p(x_{T:0})$는 Reverse Diffusion Process를 정의하는 함수이다
마찬가지로 $p(x_{T:0})$도 가우시안 분포를 따른다고 하자.
Forward Diffusion Process에서 정의했던것과 같은 논리를 따르면 $p(x_{T:0})$는 함수는 다음과 같이 정의할 수 있다.
$P(x_{T})\prod_{t=1}^{T}P(x_{t-1}|x_{t})$
다시 말해, 랜덤 가우시안을 따르는 $P(x_{T})$와 모든 중간 단계의 곱 $\prod_{t=1}^{T}p(x_{t-1}|x_{t})$이다.ELBO
적용우리의 목적은 Reverse 과정을 거쳐 도출된 원본(에 가장 가까운 Latent)
$x_{0}$를 재구성하여 원본 이미지로 복원하는 함수 $p(X_{0})$의 우도(Likelihood)가 최대화가 되길 원한다.
마코프 체인의 형식을 빌려오면, 이는 다음과 같이 정의할 수 있다.
$p(x_{0}) = \int_{z} p(x_{t-1}|x_{t}) = \int_{z}P(x_{T})\prod_{t=1}^{T}P(x_{t-1}|x_{t})$
문제는, $P(x_{0})$의 를 직접 계산하여 최대 우도를 구하는것은 $\prod_{t=1}^{T}P(x_{t-1}|x_{t})$라는 항에 의해 T....1 시점의 모든 Hidden State들을 고려하여 적분해야하기 때문에 사실상 불가능한 연산 이라는 점이다.
그래서, 변분추론에서 자주 쓰이는 테크닉인 ELBO를 활용해 상한을 정의하는 방식을 대신 활용한다.
$E[-log p(x_{0})] \leq E_{q}[-log\frac{p(x_{T:0})}{q(x_{1:T|x_{0}})}]) = E_{q}[-log p(x_{T}) - \sum_{t=1}^{T}\frac{p(x_{t-1}|x_{t})}{q(x_{t}|x_{t-1})}]$
마지막 항은 가운데 항을 로그의 성질을 이용하여 정리한 것이다.최소화
목표 확인Jonathan, Ajay and Pieter, 2020의 Appendix A를 참조하면, $E_{q}[-log\frac{p(x_{T:0})}{q(x_{1:T|x_{0}})}])= E_{q}[-log p(x_{T}) - \sum_{t=1}^{T}\frac{p(x_{t-1}|x_{t})}{q(x_{t}|x_{t-1})}]$는
다음과 같은 항으로 정리할 수 있다.
$E_{q}[-log\frac{p(x_{T:0})}{q(x_{1:T}|x_{0})}]) = E_{q}[\mathbb{KL}(q(x_{T}|x_{0}) || p(x_{T})) + \sum_{t=1}^{T}\mathbb{KL}(q(x_{t-1}|x_{t}, x_{0})||p(x_{t-1}|x_{t})]$
이 때, $\mathbb{KL}$은 쿨벡-라이블러 발산을 의미하고, 우변 첫번째 항은 Jonathan et.al의 $L_{T}$항을, 두번째 항은 $L_{t-1}$항과 일치한다.
우변의 첫번째 항은
① 임의의 가우시안에서 추출한 상수 $x_{T}$와
② 마찬가지로 상수 $x_{T}$, 상수 $\alpha_{t}$, 상수 $\sigma_{t}$에 의존하는 $N(x_{t}|\alpha_{t}x_{0}, \sigma_{t}^{2}\mathbb{I})$의 상수 실현값에 불과하므로 단지 상수항에 불과하다.
결국, 우변의 두번째 항을 최소화 해야 전체적인 손실함수가 최소화될 수 있다.손실함수
정의따라서, 두번째 항을 정리하여 손실함수로 삼으면, 이를 이용하여 학습을 수행할 수 있다.
① 우선 베이지안 규칙을 적용하여 $q(x_{t-1}|x_{t}, x_{0})$를 다음과 같이 표현할 수 있다.
$q(x_{t-1}|x_{t}, x_{0}) = q(x_{t}|x_{t-1}, x_{0}) \cdot \frac{q(x_{t-1}|x_{0})}{q(x_{t}|x_{0})}$
기본 개념 정의 ②의 Forward Diffusion Process를 정의하는 함수에서
$q(x_{t}|x_{t-1})$는 $N(x_{t} | \alpha_{t}x_{t-1}, \sigma_{t}^{2}\mathbb{I})$ 형태의 정규분포를 따름을 정의하였다.
$q(x_{t}|x_{t-1}, x_{0})$는 기본 형태 $q(x_{t}|x_{t-1})$ 에서 $x_{0}$ 조건부를 추가하고 $\frac{q(x_{t-1}|x_{0})}{q(x_{t}|x_{0})}$를 결합한 형태인데,
베이지안 추론에 따르면 사전분포 $q(x_{t}|x_{t-1}, x_{0})$와 데이터 우도 분포 $\frac{q(x_{t-1}|x_{0})}{q(x_{t}|x_{0})}$가 모두 정규분포면,
켤레 사전분포 관계에 따라 사후분포도 정규분포이다.
이 사실을 이용하여 $q(x_{t-1}|x_{t}, x_{0})$라는 사후분포의 분포를 추론하면 (아마도) 아래와 같은 형태로 표현 가능할것이다.
$q(x_{t-1}|x_{t}, x_{0}) = N(x_{t-1}|\mu_{\theta}(x_{t}, t), \overline{\sigma}_{t}\mathbb{I})$
일단, 지금 단계에서 알 수 없는 평균과 분산의 함수는 일단 $\mu_{\theta}(x_{t},t)$와 $\overline{\sigma}_{t}$로 두었다.
Diederik et.al, 2021에 따르면(Appendix E) $\mu_{\theta}(x_{t},t)$와 $\overline{\sigma}_{t}$는 다음과 같이 정리할 수 있다.
$\mu_{\theta}(x_{t},t) = \frac{\alpha_{t|t-1}\sigma^{2}_{t-1}}{\sigma_{t}^{2}}x_{t} + \frac{\alpha_{t-1}\sigma_{t|t-1}^{2}}{\sigma_{t}^{2}}x_{0}$,
$\overline{\sigma}_{t} = \frac{\sigma_{t-1}^{2}}{\sigma_{t}^{2}}$
(단, $\alpha_{t|s} = \frac{\alpha_{t}}{\alpha_{s}}$, $\sigma_{t|s}^{2} = \sigma_{t}^{2}-\alpha_{t|s}^{2}\cdot\sigma_{s}^{2}$으로 정의한다.
② $\mathbb{KL}(P||Q) = \sum_{i} p(i) \cdot log\frac{p(i)}{q(i)}$ 이고,
Diederik et.al, 2021의 Appendix E의 논리 전개를 따라 해당 쿨백-라이블러 발산 꼴을 정리하면
$\mathbb{KL}(q(x_{t-1}|x_{t}, x_{0})||p(x_{t-1}|x_{t})) = \frac{1}{2}(\frac{\alpha_{t-1}^{2}}{\sigma_{t-1}^{2}} - \frac{\alpha_{t}^{2}}{\sigma_{t}^{2}})||x_{0} - x_{0,\theta}||^{2}$
③ 한편, $x_{0}$에서 파생된것처럼 보이는 $x_{0,\theta}$가 갑자기 등장하였는데,
이는 파라미터 $\theta$를 가지는 일종의 학습 가능한 확률변수이다.
가우시안 노이즈 $\epsilon$이 학습 불가능하다는 점을 해결하기 위한 테크닉인
'Reparametrization Trick'을 다루기 위해 등장한 것인데, 아래에 설명한다.
====================================================================
한편, '수식 개념 정의'에서 우리는 $x_{t}$를 다음과 같이 나타내도록 정의하였다.
$x_{t} = \alpha_{t}x_{0} + \sigma_{t}\epsilon$
한편, ELBO를 이용하여 손실함수를 정의하는 데에는 한가지 치명적인 단점이 있는데,
바로 랜덤 가우시안 $\epsilon$의 존재이다. 이는 학습이 불가능한 임의의 랜덤변수로,
역전파 시 그레디언트를 구할 수 없어 결국엔 학습 실패로 이어지게 한다.
따라서, 이를 해결하기위해 상수 $\epsilon$을 임의의 학습 가능한 신경망으로 대체하는데,
이를 reparameterization Trick이라고 한다.
$\epsilon$을 학습 가능한 신경망 $\epsilon_{\theta}(x_{t},t))$로 대체하면
$x_{t} = \alpha_{t}x_{0,\theta} + \sigma_{t}\epsilon_{\theta}(x_{t},t)$
$x_{0,\theta}$에 대한 식으로 고치면
$x_{0,\theta} = \frac{x_{t}-\sigma_{t}\epsilon_{\theta}(x_{t},t)}{\alpha_{t}}$
동등하지만, 학습이 불가능한 원본 확률변수 $x_{0}$로도 표현하면
$x_{0} = \frac{x_{t}-\sigma_{t}\epsilon(x_{t},t)}{\alpha_{t}}$
=====================================================================
((한편, 논문의 표현을 빌리자면
$\frac{\alpha_{t-1}^{2}}{\sigma_{t-1}^{2}}$ 와 $\frac{\alpha_{t}^{2}}{\sigma_{t}^{2}}$는신호대 잡음비(Signal-to-Noise Ratio, SNR)의 개념으로 나타낼 수 있고,
각각 SNR(t-1)과 SNR(t)로 쓸 수 있다. 중요한 내용은 아니지만 일단 첨언한다.))
$\frac{x_{t}-\sigma_{t}\epsilon_{\theta}(x_{t},t)}{\alpha_{t}}$를 넣고 식을 정리하면
$||x_{0} - x_{0,\theta}||^{2}$
$ = ||\frac{x_{t}-\sigma_{t}\epsilon}{\alpha_{t}} - \frac{x_{t}-\sigma_{t}\epsilon_{\theta}(x_{t},t)}{\alpha_{t}}||^{2}$
$ = ||\alpha_{t}x_{t} + \sigma_{t}\epsilon - \alpha_{t}x_{t} - \sigma_{t} \epsilon_{\theta}(x_{t},t)||^{2}$
$\approx ||\epsilon - \epsilon_{\theta}(x_{t},t)||^{2}$
근사를 수행하면서 상수항인 SNR(t), SNR(t-1) $\sigma_{t}$등은 무시하였다.결론 다시 강조하면, Diffusion Model은 원본 픽셀 공간 $x_{t}$대신 압축된 잠재공간 $z_{t}$를 대신 활용한다.
위에서 도출한 항에 $x_{t}$를 $z_{t}$로 대체한다.
$z_{0}$ ~ $\varepsilon(x_{0})$, $\epsilon$ ~ $N(0,1)$, 그리고 t는 마코프 체인의 T...1 중 t번째 프로세스라고 할 때
$L_{LDM}:= \begin{bmatrix} \left \| \epsilon - \epsilon_{\theta}(z_{t},t)) \right \|_{2} \end{bmatrix}$
단, $\left \| .\right \|_{2}$는 L2 Loss를 의미한다.
③ 위 Loss를 최소화하는 방향으로 Gradient Descent를 수행하여 학습을 수행한다.
-. Reverse diffusion Process 샘플링
학습(파인튜닝)이 완료되어 Denoiser로 변신한 U-Net은 추론 과정에서 샘플링이라고 불리우는 과정을 수행한다.
과정을 요약하면 다음과 같이 나타낼 수 있다.
① 임의의 랜덤 가우시안에서 추출한 $Z_{T} ~ N(0,I)$에서 출발한다.
② T...t번째 단계에서, $Z_{t-1}$(즉, 직전 Hidden State)를 학습 완료된 Denoiser에 통과시켜 탈 노이즈된 t번째 표현형 $Z_{t}$를 도출한다.
③ ②의 과정을 $t...1$번 반복적으로 수행함으로서 가장 원본에 가까운 Latent 표현형인 $Z_{0}$를 점차적으로, 순차적으로 복원한다.
이후, Z는 Auto Encoder의 Decoder $D$를 통과하며 원본 예측값 $\overline{x}$로 복원된다.
(4) Conditioning Mechanism

(좌) Reverse Diffusion Process 수행 구조도
(우) 학습이 완료된 Denoiser $\epsilon_{\theta}$를 이용하여 원본 복원을 수행하는 DDPM Sampling의 유사 코드
T...1의 For문을 돌면서 임의의 가우시안 $Z_{t} ~ N(0,I)$로부터 원형 Latent인 $Z_{0}$ 으로 점차적으로 복원을 수행한다.
이는 Stable Diffusion에서 쓰이는 초창기 '스케쥴러(샘플러)'중 하나인 DDPM으로,
향후 Euler나 DPM 2++ Karras같은 진보된 샘플러가 등장하여 바닐라 DDPM을 역사속으로 사라지게 만들었다.
-. 저자들은 여기서 한걸음 더 나아가 Reverse Diffusion이 특정 조건 하에서 진행되도록 조절하는 메커니즘을 하나 더 추가하는데, 여기서 조건이란 Text, Sementic map 혹은 Image 표현형 등을 가리킨다.
-. 논문에서도 채용한 Transformer를 예시로 들면, Tokenizer(논문에선 Bert Tokenizer를 채용했다고 밝히고 있다)를 통해 토큰화된 Text Prompt는 Transformer를 거쳐 문맥을 고려한 임베딩으로 변환된다.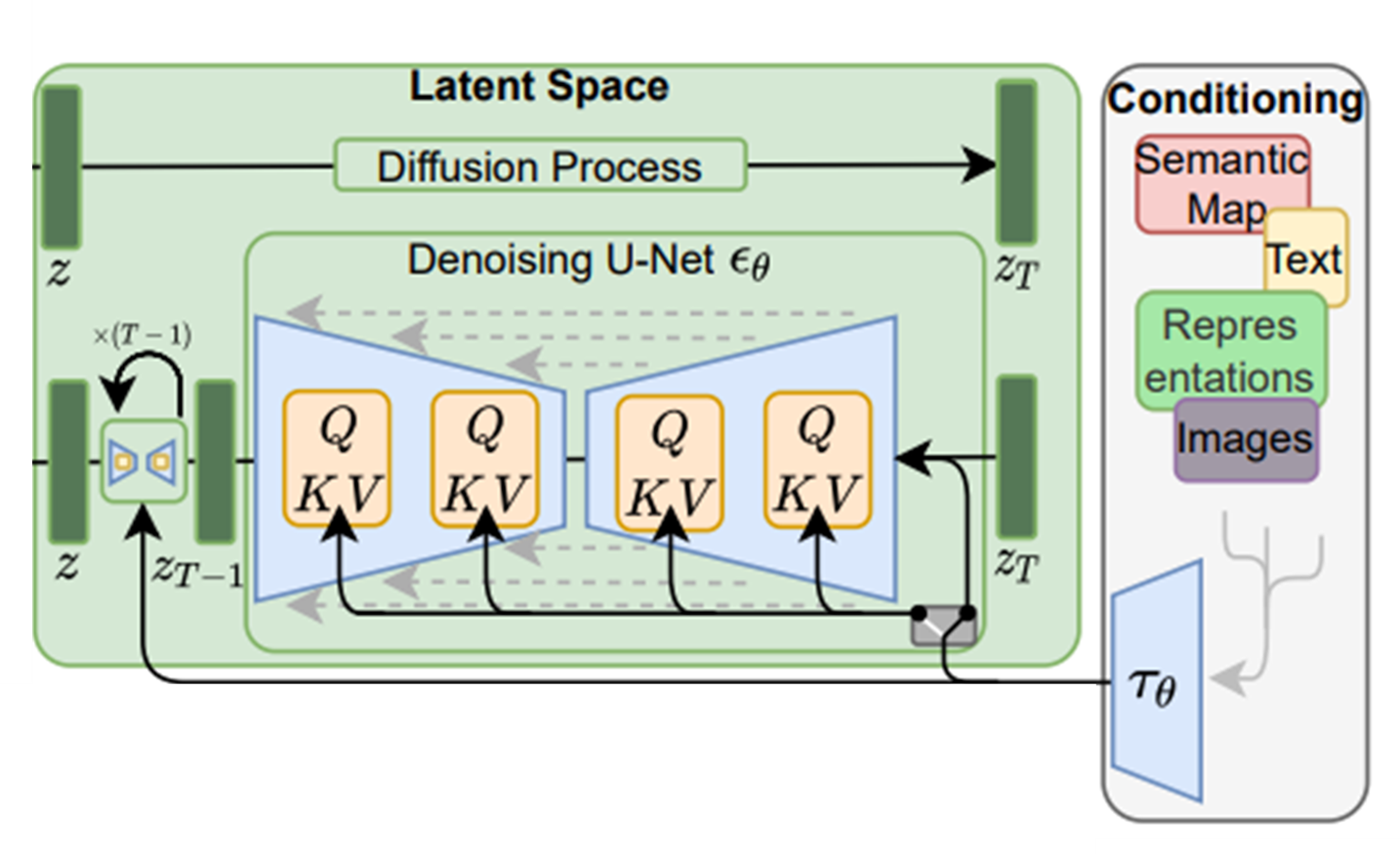
Reverse Denoising Process에 Conditioning을 주는 방법론에 대한 묘사도
컨디셔너 $\Gamma_{\theta}$를 통과한 임베딩은 Scaled dot-product attention을 통해
Denoiser의 예측된 표현형 $Z_{t}$에 첨부된다.
-. 트랜스포머를 통해 변환된 Text Prompt $y$의 임베딩을 $\Gamma_{\theta}(y)$라고 표현하자. 이 때, 이 임베딩을 Denoiser Neural network, 즉 U-Net에 반영하기 위해 저자들은 트랜스포머에서도 쓰였던 구조인 Scaled-dot Product Attention을 활용한다.
-. 컨디셔너(트랜스포머)가 추가되었기 때문에, 이제 손실함수도 컨디셔너 $\Gamma_{\theta}$가 추가되어야 한다.$\Gamma_{\theta}(y)$를 컨디셔너(트랜스포머)를 통과한 임베딩,
$\varphi_{i}(z_{t})$를 i번째 U-Net Layer를 통과중에 캐치한 중간 단계 표현형이라고 하자.
트랜스포머에서의 표현형을 빌려, Query, Key, Value를 다음과 같이 정의하자.
$Q = W_{Q}^{(i)} \cdot \varphi_{i}(z_{t})$
$K = W_{K}^{(i)} \cdot \Gamma_{\theta}(y)$
$V = W_{V}^{(i)} \cdot\Gamma_{\theta}(y)$
(이 때, $W_{V}^{(i)} \in \mathbb{R}^{d \times d_{\epsilon}^{(i)}}$,$W_{Q}^{(i)} \in \mathbb{R}^{d \times d_{\Gamma}}$, $W_{K}^{i} \in \mathbb{R}^{d \times d_{\Gamma}}$)
$Attention(Q,K,V) = softmax(\frac{QK^{T}}{\sqrt{d}})\cdot V$
를 i개의 레이어를 거쳐서 나온 최종 표현형을
$z_{t-1} = \epsilon_{\theta}(z_{t})$ 로 한다.
2) 실험 결과$z ~ \varepsilon(x)$,
$\epsilon ~ N(0,1)$,
$y$는 컨디셔너에 투입되는 조건,
$\Gamma_{\theta}(y)$를 $y$의 임베딩,
그리고 t는 마코프 체인의 T...1 중 t번째 프로세스라고 할 때
$L_{LDM}:= \begin{bmatrix} \left \| \epsilon - \epsilon_{\theta}(z_{t},t,\Gamma_{\theta}(y))) \right \|_{2} \end{bmatrix}$
단, $\left \| .\right \|_{2}$는 L2 Loss를 의미한다.
(1) 저자들이 실험을 채용한 Metric은 다음과 같다.
(2) 저자들은 우선적으로 AutoEncoder의 적절한 압축 파라미터 f를 찾는 실험을 수행한다.Metric 설명 비고 FID 사전 학습된 Inception V3 모델을 통해 예측한 이미지 표현형을 이용한 거리 함수
실제 이미지를 Inception V3에 통과시켜 얻은 이미지 표현형 벡터 $\overrightarrow{R}$, ($\overrightarrow{R} \in \mathbb{R}^{N}$)과
생성된 이미지를 Inception V3에 통과시켜 얻은 이미지 표현형 벡터$\overrightarrow{G}$, ($\overrightarrow{G} \in \mathbb{R}^{N}$)이 있다고 할 때, FID는
$|\mu_{\overrightarrow{R}} - \mu_{\overrightarrow{G}}|^{2} + tr(\Sigma_{\overrightarrow{R}} + \Sigma_{\overrightarrow{G}} - 2(\Sigma_{\overrightarrow{R}} \cdot \Sigma_{\overrightarrow{G}})^{(1/2)})$
이 때, $\mu$는 각 벡터의 평균, $\Sigma$는 각 벡터의 (공)분산 행렬을 의미한다.
값이 낮을수록 생성된 이미지가 실제 이미지에 근접했다고 여긴다.낮을수록
고성능Precision 실제 이미지의 임베딩과 생성된 이미지의 임베딩이 존재할 때
실제 이미지 임베딩의 k-Nearest Neighbor 세트 안에 포함된
생성된 이미지 임베딩이 포함된 갯수높을수록
고성능Recall 실제 이미지의 임베딩과 생성된 이미지의 임베딩이 존재할 때
생성된 이미지 임베딩의 k-Nearest Neighbor 세트 안에 포함된
실제 이미지 임베딩이 포함된 갯수높을수록
고성능

1 ~ 32까지의 f값을 기준으로 Train Step에 따른 FID(좌), IS(우)
무압축(LDM-1)일때 전반적으로 성능이 우수하고, 가장 압축을 많이 했을때(LDM-32)
성능이 가장 떨어지는 것을 확인 가능하다.

1 ~ 32까지의 f값을 기준으로 FID vs 초당 샘플링속도(throughput)
CalebA(좌) 이미지 세트와 ImageNet(우) 이미지 세트에서의 실험
각 선들의 네모난 Marker는 200,100,50,20,10번의 Sampling Step을 의미한다.
전반적으로 f가 높아질수록 초당 처리하는 샘플의 수가 늘어나는 것을 확인할 수 있다.
(오른쪽으로 퍼질수록 각 Sampling Step에서 초당 처리 가능한 샘플수가 많아짐을 의미한다.)
그러나, 그 반대 급부로 성능인 log FiD는 LDM-32에서의 예외를 제외하고 낮아지는 것을 확인 가능하다.
결론적으로, LDM-4와 LDM-8이 가장 적당한 성능과 가장 적당한 처리 속도를 보이는 것을 확인 가능하다.
(3) 다음으로 저자들은 다양한 SOTA 벤치마크 모델들을 놓고 조건이 주어지지 않았을 때 FID, Precision, Recall에 기반한 성능 테스트를 수행한다.
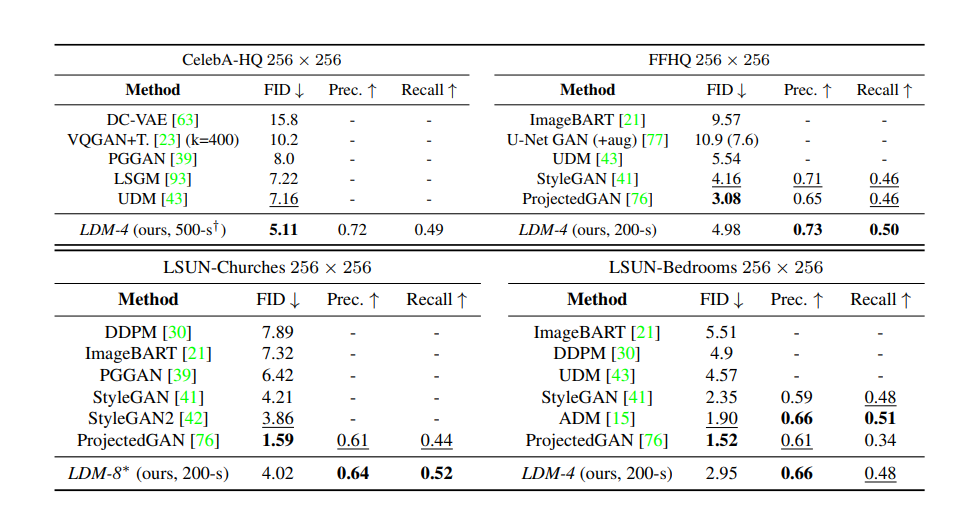
CelebA-HQ, FFHQ, LSUN_Churches, LSUN-Bedrooms 데이터 세트에 대한 벤치마크 결과
LSUN-Bedrooms에선 ADM에 밀린 결과를 보여주지만, Latent Diffusion은 ADM의 절반에 파라미터와
1/4로 축소된 학습시간을 가졌다는 점에 비춰볼때 사실상 압도했다고 해석할 수 있다.
(4) 마지막으로, 저자들은 다양한 Text Prompt를 조건으로 부여한 데이터셋을 대상으로 다양한 SOTA 모델들에 대한 벤치마크를 수행한다.

MS-COCO 데이터셋으로 수행한 Diffusion 계열의 SOTA 모델들과 LDM 모델의 성능 벤치마크 결과
LDM-KL-8은 KL-Regularization을 적용한 후 f=8임을 의미하고,
*-G는 Classifier Free Guidance(CFG)를 적용한 버전을 의미한다.
(Classifier Free Guidance는 추후에 다루기로 한다.)
4종의 Diffusion SOTA모델들을 상대로, 더 적은 파라미터를 가진 LDM이 비등하거나, 더 좋은 성능을 기록했다.

Text와 이미지의 짝으로 이루어진 LAION 데이터셋에 대한 LDM의 출력 결과
200 step(DDIM, $\eta = 1.0$)으로 샘플링을 하였고, CFG 파라미터는 10으로 설정하였다.
<참고문헌>
- Robin Rombach et.al, "High-Resolution Image Synthesis with Latent Diffusion Models", Computer Vision and Pattern Recognition(IEEE, 2022), page 10684-10695.
- Jonathan, Ajay and Pieter, "Denoising Diffusion Probabilistic Models", Advances in Neural Information Processing System 33(NIPS, 2020), page 6840-6851
- Diederik et.al, "Variational Diffusion Models", arxiv, https://arxiv.org/pdf/2107.00630.pdf, 2021.
- "What are Diffusion Models?", https://lilianweng.github.io/posts/2021-07-11-diffusion-models/, 2024-03-17 확인
- Ayush Thakur, "How to Evaluate GANs using Frechet Inception Distance(FID)", How to Evaluate GANs using Frechet Inception Distance (FID) | gan-evaluation – Weights & Biases (wandb.ai), 2024-03-17 확인
- Wikipedia, "Diffusion", https://en.wikipedia.org/wiki/Diffusion, 2024-03-17 확인
- "Improved Precision and Recall", https://hichoe95.tistory.com/118, 2024-03-17 확인


