Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #야코비 회전법 #QR법 #하우스홀더반사 #행렬회전
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #고유분해
- Optimization
- 미적분 #접선의 방정식 #최적화 #뉴턴법 #뉴턴-랩슨법
- 미적분
- Marketing Mix Modeling
- 시계열분석 #Time-Series Analysis #이상탐지 #Anomaly Detection #Spectral Residual #CNN #SR-CNN
- lightweightmmm
- 미적분 #평균값 정리 #로피탈의 정리 #접선의 방정식
- mmm
- 프로그래머를 위한 선형대수 #선형대수 #행렬계산
- 프로그래머를 위한 선형대수 #선형대수 #고유분해 #고윳값 #고유벡터
- bayesian inference
- bayesian
- 수리통계
- 미적분 #사인과 코사인의 도함수
- 프로그래머를 위한 선형대수 #선형대수 #LU분해
- Media Mix Modeling
Archives
- Today
- Total
문과생 네버랜드의 데이터 창고
14-1. 감마분포의 친족분포들(카이제곱, 베타, 디리클레 분포) 본문
- 카이제곱 분포
1) $\alpha = \frac{r}{2}$, $\beta = 2$일 때의 감마분포를 가지는 확률변수 X를 카이제곱분포라고 한다.
${(1})$ 즉, 아래의 pdf를 가진다.
$f(x) = \begin{cases}
\frac{1}{\Gamma(\frac{r}{2})\cdot 2^{\frac{r}{2}}} x^{(\frac{r}{2}-1)} \cdot e^{-\frac{x}{2}} & \text{ if } 0 < x < \infty\\
0 & \text{ else }
\end{cases}$
2) 카이제곱분포의 MGF와 이를 이용한 기댓값, 분산은 아래와 같다.
${(1})$ $M(t) = (1-2t)^{-\frac{r}{2}}$, $t < \frac{1}{2}$
${(2)}$ $E(x)$
-. $\frac{d(1-2t)^{-\frac{r}{2}}}{dt}|_{t=0} = -\frac{\gamma}{2}(1-2\cdot 0)^{-\frac{\gamma + 2}{2}} \cdot (-2) = \gamma$
${(3)}$ $Var(x)$
-. $M''(0) = \gamma(\gamma +2)(1 - 2t)^{-\frac{\gamma}{2} - 2}|_{t = 0} = r^{2} + 2r$
-. 따라서 $Var(x) = r^{2} + 2r - r^{2} = 2r$
3) 카이제곱분포의 기타 성질
${(1)}$ 감마분포의 특수한 경우기 때문에 감마분포의 가법성은 카이제곱 분포에서도 그대로 유지된다.
${(2)}$ 1,2,....,k에 대하여 일반화된 기댓값 공식이 존재한다. 이는 뒤에서 몇번 활용될 계획이므로 숙지하고 넘어가자.
${(3)}$ 정규분포를 따르는 확률변수의 2차형식의 변환확률변수는 카이제곱분포를 따른다.(매우 중요)X ~ $x^{2}(r)$ 이라고 하자. k에 대하여 $k > -\frac{r}{2}$가 성립한다고 하자.
$$E(x^{k}) = \int_{0}^{\infty}\frac{1}{\Gamma(\frac{r}{2})2^{\frac{r}{2}}}x^{\frac{r}{2} + k - 1}exp(-\frac{x}{2})dx$$
이 때, $u = \frac{x}{2}$로 변수변환을 수행하면 |J| = 2이고, 따라서
$$E(x^{k}) = \int_{0}^{\infty}\frac{1}{\Gamma(\frac{r}{2})2^{\frac{r}{2}-1}}2u^{\frac{r}{2} + k - 1}exp(-u))du$$
$$ = \frac{2^{\frac{r}{2}+k-1}}{\Gamma(\frac{r}{2})2^{\frac{r}{2}-1}} \int_{0}^{\infty}u^{\frac{r}{2} + k - 1}exp(-u)du $$
이 때, 적분식 안은 $\Gamma(\frac{r}{2} + k)$와 같으므로, 식을 다시 정리하면
$$E(x^{k}) = \frac{2^{k}\Gamma(\frac{r}{2} + k)}{\Gamma(\frac{r}{2})}$$확률변수 X가 $N(\mu, \sigma^{2})$ 정규분포를 따르는 확률변수라 하자. 이 때,
$$V = \frac{(X - \mu)^{2}}{\sigma^{2}}$$
인 확률변수 V는 $X^{2}(1)$을 따른다.$W = \frac{(x - \mu)}{\sigma}$가 N(0,1)인 표준정규분포를 따름을 정규분포에서 보였다.
$V = W^{2}$이므로, 확률변수 V의 cdf를 $G(V)$라고 정의하면
$G(v) = p(W^{2} \leq v) = p(-\sqrt{v} \leq W \leq \sqrt{v})$ 는 참이다.
이를 적분형식으로 나타내면
$$G(v) = 2\int_{0}^{\sqrt{v}}\frac{1}{\sqrt{2\pi}}exp(-w^{2}/2)dw$$ 이다.
(단, 정규분포의 pdf는 좌우대칭인점을 이용하여 $0 ~ \sqrt(v)$ 구간에 대해서만 구했다.)
$w = \sqrt{y}$로 변수변환을 수행하면 그 야코비안 $|J| = \frac{\partial w}{\partial y} = \frac{1}{2\sqrt{y}}$ 이고
$$G(v) = \int_{0}^{v}\frac{1}{\sqrt{2\pi}\sqrt{y}}exp(-y/2)dy$$
이를 미분하면 pdf를 도출할 수 있으므로 $\frac{\partial G(v)}{\partial y} = g(v)$는 미적분의 기본정리에 따라
$g(v) = \frac{1}{\sqrt{2\pi}}v^{1/2 -1}exp(-v/2)$ 이다.
한편, $\sqrt{\pi} = \Gamma(\frac{1}{2})$와 같음이 이미 알려져있다.
$$g(v) = \frac{1}{\Gamma(\frac{1}{2})2^{(1/2)}}v^{1/2 -1}exp(-v/2)$$
는 $X^{2}(r=1)$를 따르는 확률변수의 pdf이므로, 이로서 증명되었다. - 베타분포
1) 결합 pdf $f(x_{2}, x_{2})$가 독립인 두 확률변수 $x_{1}$, $x_{2}$의 결합 pdf라고 할 때
${(1)}$ $X_{1}$, $X_{2}$가 각각 $\Gamma(\alpha)$, $\Gamma(\beta)$를 따른다고 한다면
-. $h(x_{1}, x_{2}) = \begin{cases}
\frac{1}{\Gamma(\alpha)\Gamma(\beta)} \cdot x_{1}^{\alpha - 1} x_{2}^{\beta - 1} e^{-x_{1}} e^{-x_{2}} & \text{ if } 0 < x < \infty\\
0 & \text{ else }
\end{cases}$
${(2)}$ 이 때, $y_{1} = x_{1} + x_{2}$, 그리고 $y_{2} = \frac{x_{1}}{x_{1} + x_{2}}$로 치환하면
-. $x_{1} = y_{1}y_{2}$, $x_{2} = y_{1}(1 - y_{2})$ 이고
-. 변환 야코비안 $|J| = \begin{bmatrix}
y_{2} & y_{1}\\
(1-y_{2}) & -y_{1}
\end{bmatrix} = -y_{1}y_{2} - y_{1}(1-y_{1}) = -y_{1}$
-. 변환 야코비안을 포홤하여 결합 pdf를 최종 정리하면
$$ pdf(y_{1}, y_{2}) = \frac{1}{\Gamma(\alpha)\Gamma(\beta)}[y_{1}y_{2}]^{\alpha - 1}[y_{1}(1-y_{2})]^{\beta - 1}e^{-y_{1}}|-y_{1}|$$ $$= \frac{1}{\Gamma(\alpha)\Gamma(\beta)}y_{1}^{\alpha + \beta - 1}y_{2}^{\alpha - 1}(1-y_{2})^{\beta - 1}e^{-y_{1}} $$
이다.
${(3)}$ 이제, $y_{2}$에 대한 주변 확률분포의 pdf를 구하면
-. $f(y_{2}) = \int_{0}^{\infty} \frac{1}{\Gamma(\alpha)\Gamma(\beta)}y_{1}^{\alpha + \beta - 1}y_{2}^{\alpha-1}(1-y_{2})^{\beta-1}e^{-y_{1}}dy_{1}$
-. 위 식은 상수항을 빼면 $f(y_{2}) = \frac{y_{2}^{\alpha-1}(1-y_{2})^{\beta-1}}{\Gamma(\alpha)\Gamma(\beta)} \int_{0}^{\infty} y_{1}^{\alpha + \beta - 1}e^{-y_{1}}dy_{1}$
-. 적분식은 $\Gamma(\alpha + \beta)$인 감마 함수이므로, 결합하여 정리하면
$$ g_{2}(y_{2}) = \begin{cases}
\frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}y_{2}^{\alpha-1}(1-y_{2})^{\beta-1} & \text{ if } 0 < y_{2} < 1\\
0 & \text{ else }
\end{cases} $$
이고, 이것이 바로 베타분포의 pdf이다.
2) 베타분포의 기댓값과 분산은 아래와 같다.
${(1)}$ $E(X) = \frac{\alpha}{\alpha + \beta}$
${(2)}$ $Var(X) = \frac{\alpha\beta}{(\alpha + \beta + 1)(\alpha + \beta)^{2}}$ - 디리클레 분포
1) 감마분포를 따르는 확률변수 $x_{1}, x_{2}, ... x_{k}$이 $\beta = 1$일 때
${(1)}$ 이 벡터의 총합인 $\sum x_{i}$로 정의되는, 가법성을 가지는 감마분포의 k개의 결합 분포를 디리클레 분포라고 한다.
2) 디리클레 분포 pdf의 유도
$({1)}$ $1...k$개의 서로 독립인 감마분포를 따르는 확률변수들의 결합 pdf는 아래와 같이 정의할 수 있다.
-. $f(x_{1}, x_{2}, ..., x_{k} ; \alpha_{1}, ..., \alpha_{k}) = \begin{cases}
\coprod_{0}^{k-1}\frac{1}{\Gamma(\alpha_{i})} x_{i}^{\alpha_{i} -1}e^{-x_{i}} & \text{ if } 0 < x_{i} < \infty \\
0 & \text{ else }
\end{cases} $
${(2)}$ pdf를 단순화하기 위하여 변수변환을 수행하면
-. $Y_{i} = \frac{x_{i}}{x_{1}x_{2}...x_{k+1}}$, $where (i=1,2,3,...,k)$, $y_{k+1} = x_{1},x_{2},...,x_{k+1}$ 라고 정의할 때
-. $x_{1} = y_{1}y_{k+1}, x_{2} = y_{2}y_{k+1}, ..., x_{k} = y_{k}y_{k+1}$
-. $x_{k+1} = y_{k+1}(1 - y_{1} - y_{2} - ... - y_{k})$
-. 이 때, 변환 야코비안은
$|J| = det\begin{bmatrix}
y_{k+1}& 0 & ... & 0 & y_{1}\\
0 & \ddots & \ddots & 0 & y_{2}\\
\vdots & \ddots & \ddots & \ddots & \\
0 & ... & ... & ... & \\
-y_{k+1}& ... & ... & -y_{k+1} & (1-y_{1}-...-y_{k})
\end{bmatrix}$
-. 이 때, 변환 야코비안의 마지막 행이 거슬린다. 마지막행을 없애기 위하여, 1~ (k-1)행의 요소들을 마지막 행에 지속적으로 더하면
$|J| = det\begin{bmatrix}
y_{k+1}& 0 & ... & 0 & y_{1}\\
0 & \ddots & \ddots & 0 & y_{2}\\
\vdots & \ddots & \ddots & \ddots & \\
0 & ... & ... & ... & \\
0 & ... & ... & 0 & 1
\end{bmatrix} = y^{k}_{k+1}$
${(3)}$ 변수변환 결과물을 모두 취합하여 변환 pdf를 적으면
-.
-.이제, 우리가 관심이 있는 k개까지의 분포의 결합을 확인하기 위해 $y_{k+1}$을 적분하여 없애면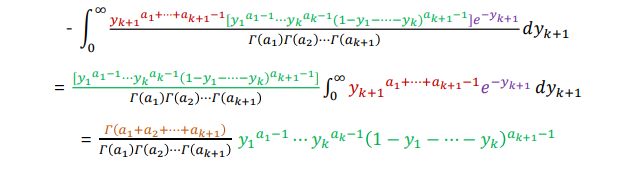
-. 이것이 바로 디리클레 분포의 pdf가 된다.
3) 디리클레 분포의 쓰임
${(1)}$ 베이즈 통계학에서, 디리클레 분포른 다항분포의 켤레사전분포이다.
-. 즉, 다항분포를 가능도 함수로 갖는 디리클레 사전 분포는 디리클레-다항분포를 생성한다.
-. 이는 NLP 분야에서 매우 광범위하게 쓰이고 있는 토픽 모델링 기법 중 가장 많이 쓰이는 알고리즘인 잠재 디리클레 할당(Latent Dirichlet Allocation, LDA)를 구성하는 핵심 분포로 활용된다.
'수리통계' 카테고리의 다른 글
| 15-1 다변량 정규분포 (0) | 2023.06.20 |
|---|---|
| 15. 정규분포 (2) | 2023.06.19 |
| 14. 감마분포 (0) | 2023.05.30 |
| 13. 푸아송 분포 (2) | 2023.05.26 |
| 12. 이항분포 (0) | 2023.05.22 |



