Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 미적분
- 미적분 #평균값 정리 #로피탈의 정리 #접선의 방정식
- 미적분 #사인과 코사인의 도함수
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #야코비 회전법 #QR법 #하우스홀더반사 #행렬회전
- lightweightmmm
- 미적분 #접선의 방정식 #최적화 #뉴턴법 #뉴턴-랩슨법
- 프로그래머를 위한 선형대수 #선형대수 #LU분해
- 프로그래머를 위한 선형대수 #선형대수 #행렬계산
- 시계열분석 #Time-Series Analysis #이상탐지 #Anomaly Detection #Spectral Residual #CNN #SR-CNN
- 수리통계
- mmm
- Marketing Mix Modeling
- bayesian inference
- bayesian
- Optimization
- Media Mix Modeling
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #고유분해
- 프로그래머를 위한 선형대수 #선형대수 #고유분해 #고윳값 #고유벡터
Archives
- Today
- Total
문과생 네버랜드의 데이터 창고
24. 카이제곱 검정 본문
-
카이제곱 검정이란
1) 카이제곱 분포에 기반한 가설검정 방법
${(1)}$ 각 명목형 데이터의 빈도(Count)를 확률변수로 취급하고, 관측값과 기댓값 사이에 유의미한 차이가 있는지를 검정
${(2)}$ 다음의 가설을 검정한다.
-. $H_{0}$ : $p_{1} = p_{10} / p_{2} = p_{20} / ... / p_{k-1} = p_{(k-1)0}$
-. $H_{1}$ : 적어도 하나는 다르다
-. 이때, $p_{k-1}$은 검정의 대상이 되는 지정된 어떤 값이다.
2) 카이제곱 검정식의 유도
${(1)}$ 2차까지의 항을 우선 구해보고, 이를 토대로 일반화된 패턴을 끌어내본다.
-. $ X_{1} $를 다변량 정규분포를 구성하는 확률변수 중 하나라고 하자.
$$ X_{1} \sim b(n, p_{1})$$ 를 정의하자.
중심극한 정리에 의하여 $n \rightarrow \infty$ 일때
$$ Y_{1} = \frac{X_{1} - np}{\sqrt{np_{1}(1-p_{1})}} \sim N(0,1)$$ 이다.
한편, $Q_{1} = Y^{2}$ 이라고 하자. 즉, 정규분포의 제곱이다.
정규분포의 제곱꼴은 $X^{2}(1)$의 분포를 따르므로, 이를 정의하면
$$Q_{1} = \frac{(X_{1} - np_{1})^{2}}{np_{1}(1 - p_{1})} $$
부분분수분해(Partial Fraction Decomposition)을 이용하여
$\frac{(X_{1} - np_{1})^{2}}{np_{1}(1 - p_{1})}$를 분리하면
$$\frac{(X_{1} - np_{1})^{2}}{np_{1}(1 - p_{1})} = \frac{(X_{1} - np_{1})^{2}}{np_{1}} + \frac{(X_{1} - np_{1})^{2}}{n(1-p_{1})}$$
-. 이제, 또다른 확률변수 $X_{2}$를 $X_{1}$과 같이 다변량 확률변수 X를 구성하는 또다른 확률변수라고 정의하자.
$X_{2} = n - X_{1}$ 이고, $p_{2} = 1 - p_{1}$이라고 하자.
이 때, 역함수는 $X_{1} = n - X_{2}$ 이고 $p_{1} = 1 - p_{2}$ 이다.
위에서 구한 부분분수 분해 꼴에다가 이 사실을 대입하면
$$\frac{(X_{1} - np_{1})^{2}}{np_{1}(1 - p_{1})} = \frac{(X_{1} - np_{1})^{2}}{np_{1}} +\frac{(X_{2} - np_{2})^{2}}{np_{2}}$$
-. 위에 대한 계산을 $[X_{3}, ..., X_{n}]$에 대하여 일반화하면 다음과 같은 선형결합으로 나타낼 수 있다.
-. $n \rightarrow \infty$ 면 이 분포는 $x^{2}(k-1)$ 분포에 점근적으로 다가간다. 즉, 우리는 자유도 (k-1)의 카이제곱 분포를 활용하여 정의된 가설을 검정할 수 있다.$$ Q_{k-1} = \sum_{i = 1}^{k} \frac{(X_{i} - np_{i})^{2}}{np_{i}} $$
(단, $X_{k} = n - (X_{1} - x_{2} - \dots - x_{k-1}) $이고 $p_{k} = 1 - p_{1} - \dots - p_{k-1}$ 이다.) - 동질성에 대한 카이제곱검정
1) 최소카이제곱추정량
${(1)}$ 검정의 대상이 되는 확률변수 $X_{i}$가 지정된 값이 아닌 추정을 해야하는 모수이고, 이 모수를 모르는 경우에는 모수를 추정할 수 있는 불편추정량을 검정에 활용하여야 한다.
${(2)}$ 검정의 대상이 되는 모수 $\theta = [X_{1}, ..., X_{j}]$ 일때(단, j는 추정량을 구한 모수의 갯수이다),
$$ Q_{k-1} = \sum_{i = 1}^{k} \frac{(X_{i} - np_{i})^{2}}{np_{i}} $$는 $x^{2}(k-j)$을 따른다.
${(3)}$ 즉, 모수를 대체한 불편추정량의 갯수만큼 $x^{2}$ 분포의 자유도를 n개씩 깎는 추정량을 최소카이제곱추정량 이라고 한다.
2) 동질성에 대한 카이제곱검정
$${(1)}$ 최소카이제곱추정량을 활용하여 동질성에 대한 카이제곱검정을 정의할 수 있다.
모수가 각각 $[n_{j}, (p_{1j}, p_{2j}, ..., p_{kj})]$인 다항분포가 있다고 하자.(단. j = [1,2])
즉, 이는 두 개의 다항분포이다.
$X_{ij}$를 각각의 경우에서 구한 빈도라고 하자.
$$ Q_{k-1} = \sum_{j = 1}^{2}\sum_{i = 1}^{k} \frac{(X_{ij} - n_{j}p_{ij})^{2}}{n_{j}p_{ij}} $$
는 두 개의 독립인 확률변수 합이고, 카이제곱의 가법성에 따라
$2 \cdot x^{2}(k - 1) = x^{2}(2k - 2)$를 따른다.
한편, 다음의 가설을 검정한다.
$H_{0} : p_{11} = p_{12} / p_{21} = p_{22} / \dots / p_{k1} = p_{k2}$
이 때, 모수 $p_{k1} = p_{k2}$는 명시적으로 알 수 없으므로, 이를 대체할 수 있는 설득력있는 추정량을 사용한다.
다항분포의 $p_{k}$ 에 대한 최대우도추정량은 $\frac{X_{i1} + X_{i2}}{n_{1} + n_{2}}$ 이고, 따라서
$$ Q_{k-1} = \sum_{j = 1}^{2}\sum_{i = 1}^{k} \frac{(X_{ij} - n_{j}p_{ij})^{2}}{n_{j}p_{ij}} = \sum_{j = 1}^{2}\sum_{i = 1}^{k} \frac{(X_{ij} - n_{j}\frac{X_{i1} + X_{i2}}{n_{1} + n_{2}})^{2}}{n_{j}\frac{X_{i1} + X_{i2}}{n_{1} + n_{2}}} $$
은 최소카이제곱추정량에 따라 자유도 [2k - 2 - (k - 1)]인
$$x^{2}(k - 1)$$ 분포를 따른다.
이 때, $$\sum_{j = 1}^{2}\sum_{i = 1}^{k} \frac{(X_{ij} - n_{j}\frac{X_{i1} + X_{i2}}{n_{1} + n_{2}})^{2}}{n_{j}\frac{X_{i1} + X_{i2}}{n_{1} + n_{2}}}$$
를 동질성에 대한 카이제곱검정이라고 한다. - 독립성에 대한 카이제곱 검정
1) 분할표
${(1)}$ 확률실험의 결과를 두 속성으로 분류한다고 하자.
- 예를 들면, 사람들을 (머리색깔과 눈색깔), 혹은 (현재 지지정당과 투표 정당) 등 두 차원의 속성으로 나눌 수 있다.
${(2)}$ 이 때, 각 분류에 따라 사람들의 빈도를 세서(Count) 기록하면 아래의 표와 같이 나타낼 수 있다.
$({3)}$ 위와 같은 표를 분할표라고 지칭한다.A당 B당 C당 D당 현재 지지정당 27 32 27 21 1년전 투표정당 34 31 33 15
-. 이 때, (A당, B당, C당, D당) 과 같이 행에 속하는 분류를 A
-. (현재 지지정당, 1년전 투표정당) 과 같이 열에 속하는 분류를 B 라고 하자.
2) 분할표를 이용한 독립성 카이제곱 검정
${(1)}$ 다음과 같이 검정에 활용되는 확률변수들을 정의하자.$P_{ij} = P(A_{i} \cap B_{j})$ 이다.
즉, 위 분할표의 예시를 가져오면 다음과 같다.
$P_{A당, 현재지지정당} = P(A당 \cap 현재지지정당)$이 때, 이 실험이 n번 반복되었다고 가정하고, $P_{i.} = P(A_{i}), P_{.j} = P(B_{j})$라고 정의하자.
그러면 다음과 같은 관계가 성립된다.
$$P_{i.} = \sum_{j = 1}^{b}p_{ij}$$
$$P_{.j} = \sum_{i = 1}^{a}p_{ij}$$
$$\sum_{i=1}\sum_{j=1}P_{ij} = \sum_{i = 1}p_{i.} = \sum_{j = 1}p_{.j} = 1$$
위 관계의 의미를 분할표로 예시화하여 나타내면 다음과 같다.
즉, (A당, B당, C당, D당) 이라는 행에 대하여 각각 확률을 계산하여 더한것과
(현재 지지정당, 1년전 투표정당) 이라는 열에 대하여 각각 확률을 계산하여 더한것은
모든 행과 열에 대하여 그 값이 1로 동일하다.이 때, 모수 $p_{ij}$를 우리가 어떤 값인지 정확하게 알 수 없으므로,
동질성 검정에서 활용하였던 최소카이제곱추정량을 마찬가지로 사용한다.
즉, $$ Q_{ab-1} = \sum_{j = 1}^{a}\sum_{i = 1}^{b} \frac{(X_{ij} - np_{ij})^{2}}{np_{ij}} $$ 에서
-. $\widehat{p}_{i.}$ 에 대한 최대우도추정량은 $\frac{\sum_{j=1}^{b}X_{ij}}{n}, i = 1, \dots , a$
-. $\widehat{p}_{.j}$ 에 대한 최대우도추정량은 $\frac{\sum_{i=1}^{a}X_{ij}}{n}, j = 1, \dots , b$
두 확률변수가 상호 독립이므로
$$\widehat{p_{ij}} = \widehat{p}_{i.} \cdot \widehat{p}_{.j} = \frac{\sum_{j=1}^{b}X_{ij}}{n} \cdot \frac{\sum_{i=1}^{a}X_{ij}}{n}$$
위를 이용하면
$$ Q_{ab-1} = Q_{ab-1} = \sum_{j = 1}^{a}\sum_{i = 1}^{b} \frac{(X_{ij} - np_{ij})^{2}}{np_{ij}} = \sum_{j = 1}^{a}\sum_{i = 1}^{b} \frac{(X_{ij} - n\frac{\sum_{j=1}^{b}X_{ij}}{n} \cdot\frac{\sum_{i=1}^{a}X_{ij}}{n})^{2}}{n\frac{\sum_{j=1}^{b}X_{ij}}{n} \cdot\frac{\sum_{i=1}^{a}X_{ij}}{n}}$$
는 자유도 (ab - 1 +(a + b - 2)인
$$x^{2}(a - 1)(b - 1)$$ 를 따르며, 이를 이용하여 검정할 수 있다.
${(2)}$ 실무 친화적인 프로시져는 다음과 같이 나타낼 수 있다.1 
각각의 행과 열에 대하여 기대 확률을 구한다.2 
각 칸에 대하여 (전체 빈도 * (각 행 기대확률 * 각 열 기대확률)) 을 통해
기대빈도를 구한다.3 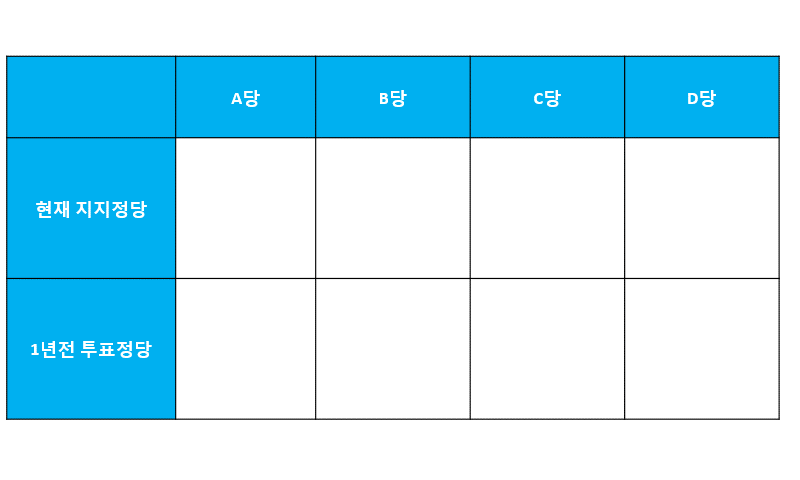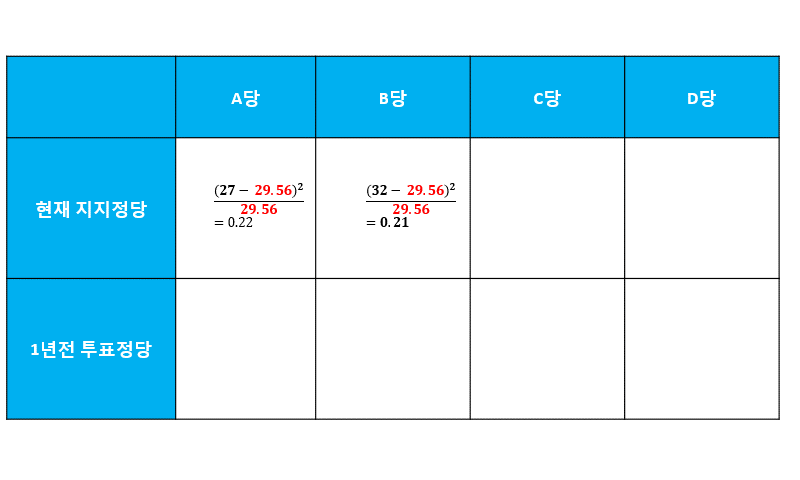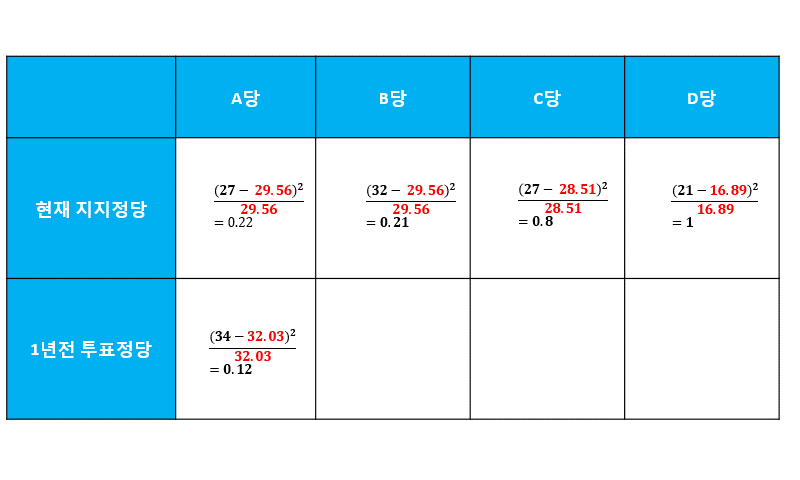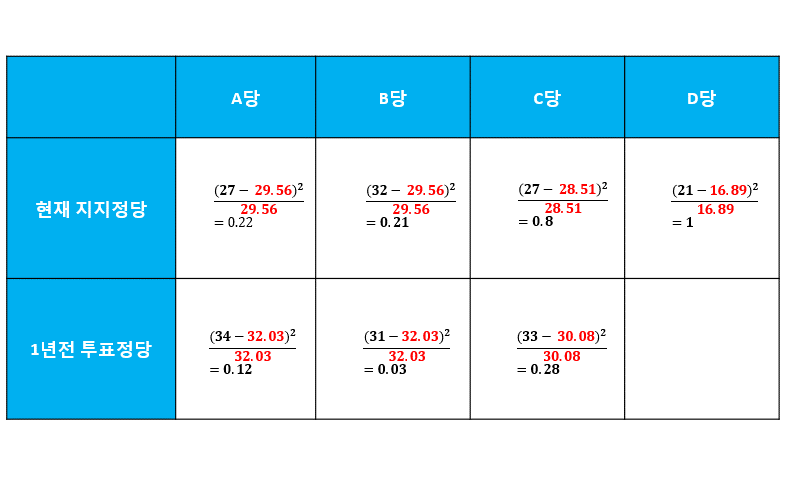
각 칸에 대하여 $\frac{(빈도값 - 기대빈도)^{2}}{기대빈도}$를 구한다.4 구한 검정통계량을 모두 더하고, 이를 카이제곱검정 임계값과 비교한다.
$$0.22 + 0.21 + 0.8 + 1 + 0.12 + 0.03 + 0.28 + 0.51 = 3.17$$
이 검정통계량은 자유도 (4-1)(2-1) = 3일때
유의 수준 $\alpha = 0.05$에서 카이제곱 임계값
$P^{-1}(x^{2}(3) = 0.05) = 3.84$
보다 작으므로, 우리는 $H_{0}$를 기각하지 못한다.
'수리통계' 카테고리의 다른 글
| 26. 통계적 부트스트랩 (0) | 2023.07.07 |
|---|---|
| 25. 몬테카를로 방법 (0) | 2023.07.06 |
| 23-1 단측검정에서 양측검정으로 일반화 (0) | 2023.07.05 |
| 23. 가설검정 (0) | 2023.07.03 |
| 22. 분위수와 Q-Q plot (0) | 2023.06.30 |



