Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 미적분 #사인과 코사인의 도함수
- lightweightmmm
- Marketing Mix Modeling
- 미적분
- 수리통계
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #고유분해
- 프로그래머를 위한 선형대수 #선형대수 #고유분해 #고윳값 #고유벡터
- 미적분 #접선의 방정식 #최적화 #뉴턴법 #뉴턴-랩슨법
- Optimization
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #야코비 회전법 #QR법 #하우스홀더반사 #행렬회전
- bayesian
- bayesian inference
- mmm
- 프로그래머를 위한 선형대수 #선형대수 #LU분해
- 프로그래머를 위한 선형대수 #선형대수 #행렬계산
- 시계열분석 #Time-Series Analysis #이상탐지 #Anomaly Detection #Spectral Residual #CNN #SR-CNN
- 미적분 #평균값 정리 #로피탈의 정리 #접선의 방정식
- Media Mix Modeling
Archives
- Today
- Total
문과생 네버랜드의 데이터 창고
31-1 다중 모수의 최대우도검정 본문
-
단변량에서 다변량으로 확장
1) 다중 모수에서의 우도비 검정
${(1)}$ $\theta = [\theta_{1}, \theta_{2}, \dots, \theta_{n}]$인 모수 벡터 $\theta$를 정의하자.
-. 이 때, 특정 모수에 대하여 연구자가 다음의 가설을 내세웠다고 하자.$[\theta_{1}, \dots, \theta_{p}]$라는 $\theta$에 부분집합에 대하여 다음은 참일 것이다
$\theta_{1} = \widehat{\theta}_{0} / , \dots, / \theta_{n-p} = \widehat{\theta}_{p}$
${(2)}$ 이와 같이 모수에 대해 어떤 주장을 내세움으로서, 모수 공간 전체에 어떤 영향을 미칠 수 있다.
-. 다중 모수(중 일부)에 대하여 어떤 가설을 주장하는 것은 전체 모수공간에 대하여 일종의 제약조건으로 작용한다.
-. 예를 들어, X가 $N(\mu, \sigma^{2})$를 따른다고 하자. 이 때, 전체 모수공간은 $\theta \in \Omega \subset \mathbb{R}^{2}$ 이다.
-. 이 때, 연구자가 $\mu = \mu_{0}$라고 주장한다고 하자. 그럼 이제 이 공간은 1차원으로 축소된다. 즉 $\theta_{0} \in \omega \subset\mathbb{R}$ 이다. 즉, 전체 모수공간의 차원을 줄였다.
${(3)}$ 한편, 연구자가 내세운 가설에 대하여 마찬가지로 우도비 검정을 정의해볼 수 있다.
-. 참모수 $\theta$를 입력받은 우도함수는 가장 높은 우도값을 내뱉는다. 여기에 대하여 우리가 정의한 $[\widehat{\theta}_{0} / , \dots, / \theta_{p} = \widehat{\theta}_{p}]$라는 가설의 부분집합을 입력받은 우도함수에 대한 비율을 정의해볼 수 있다.
-. 참모수 $\theta$를 입력받은 전체 모수공간을 $\theta \in \Omega \subset \mathbb{R}^{n}$, 가설의 부분집합을 입력받은 축소된 부분 모수공간을 $\theta_{0} \in \omega \subset\mathbb{R}^{n-p}$ 라고 정의하자. 그 우도비는 다음과 같이 정의할 수 있다.
$$\Lambda = \frac{\underset{\theta \in \Omega}{max}L(\theta)}{\underset{\theta \in \Omega}{max}L(\theta)}$$
2) 최대우도추정량을 활용한 다중모수에서의 우도비 검정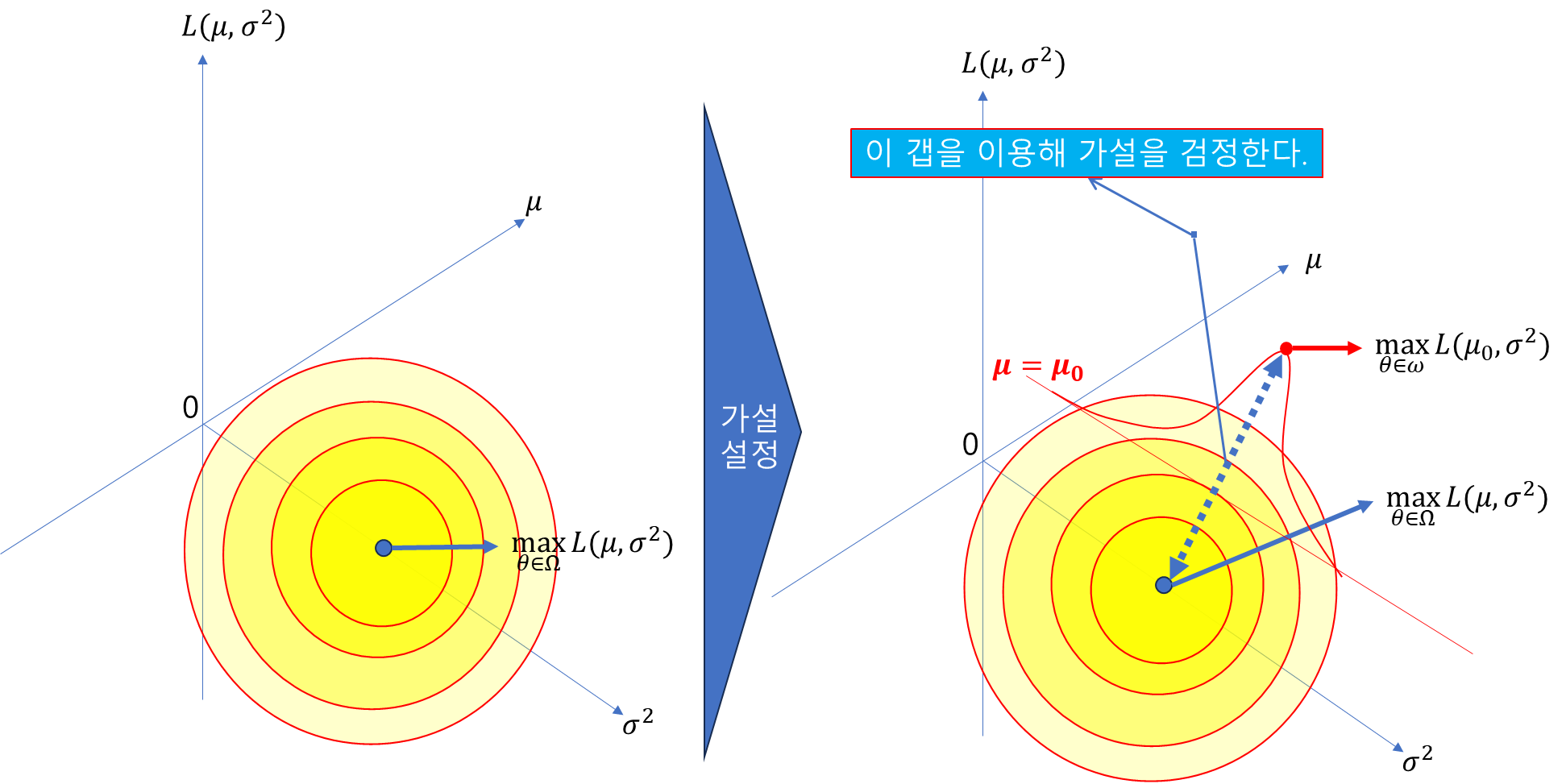
$\theta \in \Omega$에 속하는 전체 모수 공간상에서 우도함수는 참모수 $[\mu, \sigma^{2}]$에서 우도값이 최대화된다.
여기에 대하여, 연구자가 세운 가설의 공간 $\theta \in \omega$는 전체 모수공간에 비해 낮은 차원에서
나름의 우도함수를 갖게 되고, 최대화되는 점도 갖게 된다.
이 두 점 사이의 거리를 비율로서 정의하고, 가설을 검정하는 것이 다중 모수에서의 최대우도검정이 된다.
${(1)}$ 물론, 안타깝게도 우린 참모수가 뭔지 모른다. 다만 확률표본을 이용하여 생성한 통계량 중 으뜸인 최대우도추정량을 활용할 뿐이다.
-. 최대우도추정량은 전체 모수공간과 축소된 부분 모수공간에 대하여 각각 정의될 필요가 있다.위의 예시를 다시 가져오면, 연구자가 주장한 가설을 각각의 제약조건을 두면 다음과 같이 정의할 수 있다.
전체 모수의 집합 $\theta = [\theta_{1}, \theta_{2}, \dots, \theta_{n}]$에 대하여 다음의 가설을 검정한다
$H_{0} : \theta \in \omega \ VS \ H_{1} : \theta \in \Omega$
이 때, $\omega$는 가설의 제약조건에 따라서 축소된 모수공간을, $\Omega$는 전체 모수공간을 의미한다.
이 가설을 검정하기 위해, 다음의 우도비 함수를 정의한다
$$\Lambda = \frac{\underset{\theta \in \Omega}{max}L(\theta)}{\underset{\theta \in \Omega}{max}L(\theta)}$$
$\alpha = \underset{\theta \in \Omega}{max}P[\Lambda \leq c]$를 만족하는 임계값 c에 대하여
$\Lambda \leq c$이면 $H_{0}$를 기각하고 $H_{1}$을 채택
한편, 다변량 함수에서의 최대우도추정에서 정의한 방법론에 따라, $\Omega$ 와 $\omega$에 속하는 모수들을
추정하기 위해 최대우도추정량을 활용한다.
-. $\underset{\theta \in \Omega}{max}L(\theta) = L[\widehat{\Omega}]$
-. $\underset{\theta \in \omega}{max}L(\theta) = L[\widehat{\omega}]$
라고 할 때, 최대우도추정량을 활용한 우도비 검정량은 다음과 같이 정의할 수 있다.
$$\Lambda = \frac{L[\widehat{\Omega}]}{L[\widehat{\omega}]}$$
3) 다중모수에서의 우도비 검정의 특성
${(1)}$ 카이제곱 분포와의 관계
-. 단변량때와 마찬가지로 우도비 검정간에는 다음의 관계가 성립된다.$[X_{1}, \dots X_{n}]$ 을 $\theta \in \Omega \subset \mathbb{R}^{p}$에 속하는
모수 $\theta$를 가진 공통 pdf $f(X;\theta)$를 가지는 분포의 i.i.d라고 하자.
이 때, 정칙조건을 만족한다고 가정한다.
$\widehat{\theta}$를 전체 모수공간 $\Omega$에 속하는 우도함수에서 파생된 최대우도추정량이라 하고,
$\widehat{\theta}_{0}$을 모수공간이 $(p-q)$만큼 축소된 모수공간 $\omega$에 속하는 우도함수에서 파생된 최대우도추정량이라 하자. 단, q는 가설로서 내세운 모수의 갯수이다.
$$\Lambda = \frac{L[\widehat{\Omega}]}{L[\widehat{\omega}]}$$ 라고 정의할 때 다음은 참이다.
$$-2log(\lambda) \overset{D}{\rightarrow} x^{2}(q)$$
즉, $\lambda$에 대한 변환 통계량은 가설 갯수 q를 자유도로 갖는 카이제곱 분포로 분포수렴한다. - 예시로 보는 다중모수 최대우도검정
1) 정규분포 하에서의 최대우도검정
2) 다항분포 하에서의 최대우도검정$[X_{1}, \dots , X_{n}]$이 iid $N(\mu, \sigma^{2})$이라고 할 때 다음을 검정하고자 한다.
$$H_{0} : \mu = \mu_{0} \ VS \ H_{1} : \mu \neq \mu_{0}$$
-. 전체 모수공간 $\Omega$ 에서의 $L(\Omega)$를 구하면
$L(\Omega) = \prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{1}{2}(\frac{X_{i} - \mu}{\sigma})^{2})$
모수 각각에 대하여 MLE 추정량을 구하면
$$\mu_{MLE} = \frac{1}{n}\sum_{i=1}^{n}X_{i} = \overline{X} \\
\sigma_{MLE} = \frac{1}{n-1}\sum_{i=1}^{n}\sqrt{(X_{i}-\overline{X})^{2}} = S$$
$L(\Omega)$에 대하여 MLE 추정량을 삽입하면
$$\underset{\theta \in \Omega}{max}L(\theta) = L[\widehat{\Omega}] = \prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}s}exp(-\frac{1}{2}(\frac{X_{i} - \overline{X}}{s})^{2})=\frac{1}{2\pi^{n/2}} \cdot \frac{1}{(s)^{n/2}}\cdot exp(-n/2)$$
한편, 연구자가 주장하는 값 $\mu_{0}$를 넣어 축소된 $\underset{\theta \in \omega}{max}L(\theta)$를 구하면
$$\mu_{0,MLE} = \mu_{0}\\
\sigma_{0,MLE} = \frac{1}{n-1}\sum_{i=1}^{n}\sqrt{(X_{i}-\mu_{0,MLE})^{2}}$$
$$\underset{\theta \in \omega}{max}L(\theta) = L[\widehat{\omega}] = \prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}s}exp(-\frac{1}{2}(\frac{X_{i} - \mu_{0}}{\sigma_{0,MLE}})^{2})=\frac{1}{2\pi^{n/2}} \cdot \frac{1}{(\sigma_{0,MLE})^{n/2}}\cdot exp(-n/2)$$
$\Lambda$를 다음과 같이 정의한다.
$$\Lambda = \frac{L[\widehat{\Omega}]}{L[\widehat{\omega}]} = \frac{\frac{1}{2\pi^{n/2}} \cdot \frac{1}{(s)^{n/2}}\cdot exp(-n/2)}{\frac{1}{2\pi^{n/2}} \cdot \frac{1}{(\sigma_{0,MLE})^{n/2}}\cdot exp(-n/2)} = [\frac{\sigma_{0,MLE}}{s}]^{2/n} = [\frac{\sum_{i=1}^{n}\sqrt{(X_{i}-\mu_{0})^{2}}}{\sum_{i=1}^{n}\sqrt{(X_{i}-\overline{X})^{2}}}]^{2/n}$$
$$-2log(\lambda) \overset{D}{\rightarrow} x^{2}(1)$$을 이용하여 이제 가설을 검정할 수 있다.삼항분포의 pdf를 다음과 같이 정의하자
$$f(x_{1}, x_{2};p_{1},p_{2}) = p_{1}^{x_{1}} \cdot p_{2}^{x_{2}} (1 - p_{1} - p_{2})^{(n - x_{1} - x_{2})}$$
여기서 추출한 확률표본을 다음과 같이 정의하자.
$[(X_{11}, X_{21}), (X_{12}, X_{22}), \dots , (X_{1n}, X_{2n})]$
다음의 가설을 검정하고자 한다.
$$H_{0} : p_{1} = p_{2} \ VS \ H_{1} : p_{1} \neq p_{2}$$
-. 전체 모수공간 $\Omega$에 대하여 $L(\Omega)$를 구하면
$$L(\Omega) = \prod_{i=1}^{n}p_{1}^{x_{1n}} \cdot p_{2}^{x_{2n}} (1 - p_{1} - p_{2})^{(n - x_{1n} - x_{2n})}$$
-. 모수 각각에 대하여 MLE 추정량을 구하면
$$p_{1} : \widehat{p}_{1} = \frac{\sum_{i=1}^{n}X_{1n}}{n} \\ p_{2} : \widehat{p}_{2} = \frac{\sum_{i=1}^{n}X_{2n}}{n}$$
$L(\Omega)$에 대하여 MLE 추정량을 삽입하면
$$\underset{\theta \in \Omega}{max}L(\theta) = L[\widehat{\Omega}] \\ = \prod_{i=1}^{n}\widehat{p}_{1}^{x_{1n}} \cdot \widehat{p}_{2}^{x_{2n}} (1 - \widehat{p}_{1} - \widehat{p}_{1})^{(n - x_{1n} - x_{2n})} \\ = \widehat{p}_{1}^{\sum_{i=1}^{n}x_{1n}} \cdot \widehat{p}_{2}^{\sum_{i=1}^{n}x_{2n}} (1 - \widehat{p}_{1} - \widehat{p}_{1})^{\sum_{i=1}^{n}(n - x_{1n} - x_{2n})} \\ = \widehat{p}_{1}^{n\widehat{p}_{1}} \cdot \widehat{p}_{2}^{n\widehat{p}_{2}} (1 - \widehat{p}_{1} - \widehat{p}_{1})^{n(1 - \widehat{p}_{1} - \widehat{p}_{2})}$$
한편, 연구자가 주장하는 $p_{1} = p_{2}$를 반영하여 축소된 $\underset{\theta \in \omega}{max}L(\theta)$를 구하면
$p = p_{1} = p_{2}$ 에서
$$L(\omega) = \prod_{i=1}^{n}p^{x_{1n}} \cdot p^{x_{2n}} (1 - 2p)^{(n - x_{1n} - x_{2n})} \\ = p^{\sum_{i=1}^{n}x_{1n}} \cdot p^{\sum_{i=1}^{n}x_{2n}} (1 - 2p)^{\sum_{i=1}^{n}(n - x_{1n} - x_{2n})}$$
이 때, $T_{1} = \sum_{i=1}^{n}X_{1n}$으로, $T_{2} =\sum_{i=1}^{n}X_{2n}$ 으로 정의하자.
그럼
$L(\omega) = p^{T_{1} + T_{2}}(1 - 2p)^{n(1 - T_{1} - T_{2})}$ 이다.
이 떄, p에 대하여 최대우도추정량을 구하면
$\frac{\partial l(\omega)}{\partial p} = \frac{T_{1} + T_{2}}{p} - \frac{n-T_{1}-T_{2}}{1-2p} = 0$에서
$$\widehat{p} = \frac{T_{1} + T_{2}}{2n} = \frac{\widehat{p}_{1} + \widehat{p}_{2}}{2}$$
따라서, 이 최대우도추정량을 투입한 축소 모수공간의 최대우도함수는 다음과 같다.
$$L(\widehat{\omega}) = (\frac{\widehat{p}_{1} + \widehat{p}_{2}}{2})^{T_{1} + T_{2}}(1 - 2(\frac{\widehat{p}_{1} + \widehat{p}_{2}}{2})^{n(1 - T_{1} - T_{2})} = \frac{(\widehat{p}_{1} + \widehat{p}_{2})^{n(\widehat{p}_{1} + \widehat{p}_{2})}}{2}(1-\widehat{p}_{1} + \widehat{p}_{2})^{n(1-\widehat{p}_{1} + \widehat{p}_{2})}$$
이제, 우도비함수를 정의하면
$$\Lambda = \frac{L[\widehat{\Omega}]}{L[\widehat{\omega}]} = \frac{\widehat{p}_{1}^{\widehat{p}_{1}} \cdot \widehat{p}_{2}^{\widehat{p}_{2}} (1 - \widehat{p}_{1} - \widehat{p}_{1})^{n(1 - \widehat{p}_{1} - \widehat{p}_{2})}}{\frac{(\widehat{p}_{1} + \widehat{p}_{2})^{n(\widehat{p}_{1} + \widehat{p}_{2})}}{2}(1-\widehat{p}_{1} + \widehat{p}_{2})^{n(1-\widehat{p}_{1} + \widehat{p}_{2})}} = [\frac{2\widehat{p}_{1}}{\widehat{p}_{1} + \widehat{p}_{2}}]^{n\widehat{p}_{1}} \cdot [\frac{2\widehat{p}_{2}}{\widehat{p}_{1} +\widehat{p}_{2}}]^{n\widehat{p}_{2}}$$
$$-2log(\lambda) \overset{D}{\rightarrow} x^{2}(1)$$을 이용하여 이제 가설을 검정할 수 있다.
'수리통계' 카테고리의 다른 글
| 33. 충분통계량 (1) | 2023.07.21 |
|---|---|
| 32. EM 알고리즘(with GMM) (2) | 2023.07.20 |
| 19-1 다변량 함수에서의 최대우도추정 (0) | 2023.07.18 |
| 31. 최대우도검정 (0) | 2023.07.17 |
| 30. 라오-크래머 한계와 효율성 (0) | 2023.07.14 |

