Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- bayesian inference
- Optimization
- 미적분 #접선의 방정식 #최적화 #뉴턴법 #뉴턴-랩슨법
- 미적분 #평균값 정리 #로피탈의 정리 #접선의 방정식
- Media Mix Modeling
- 미적분
- 프로그래머를 위한 선형대수 #선형대수 #고유분해 #고윳값 #고유벡터
- lightweightmmm
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #야코비 회전법 #QR법 #하우스홀더반사 #행렬회전
- 프로그래머를 위한 선형대수 #선형대수 #행렬계산
- Marketing Mix Modeling
- 수리통계
- 미적분 #사인과 코사인의 도함수
- 시계열분석 #Time-Series Analysis #이상탐지 #Anomaly Detection #Spectral Residual #CNN #SR-CNN
- bayesian
- 프로그래머를 위한 선형대수 #선형대수 #LU분해
- 프로그래머를 위한 선형대수 #선형대수 #고유값 #고유벡터 #고유분해
- mmm
Archives
- Today
- Total
문과생 네버랜드의 데이터 창고
32. EM 알고리즘(with GMM) 본문
- 기댓값 최대화 알고리즘이란?
1) 지금까지 관측된 확률표본 $[X_{1}, \dots, X_{n}]$을 이용하여 최대우도추정량을 구한뒤, 이를 이용하여 추정이나 검정을 수행하는 방법론을 살펴보았다.
2) 문제는, 현실의 대다수의 문제는 현실에서 실제로 관측되지 않은 많은 확률변수에 의존한다는 것이다.
${(1)}$ 기계 장치가 여전히 가동중인 상태에서 최대우도추정을 수행해야하는 상황
${(2)}$ 수집한 몇몇 데이터가 누락되어 있는 상황에서 최대우도추정을 수행해야 하는 상황
3) 이런 경우, 관측되지 않은 확률변수도 식에 포함하여 완전한 우도함수를 구해 최대우도추정량을 구해야한다.
${(1)}$ 그러나 이런 경우 다음의 문제가 발생하게 된다.
-. 관측된 확률변수들과 잠재된 확률변수간에 (보통)깊은 연관관계가 존재하여 그 미분꼴을 닫힌 형태로 구할 수 없다
4) 위와 같은 문제가 발생했을 때, 굳이 이를 어렵게 닫힌꼴로 구하지 않고, 수치적인 알고리즘으로 수렴한 값을 구하는 방법론을 택할 수 있다.
${(1)}$ 수치적인 알고리즘을 활용하여 수렴된 해를 구하는 반복 알고리즘을 EM 알고리즘이라고 한다. - EM 알고리즘의 개념과 유도
1) 들어가기에 앞서, 다음의 개념들을 우선 정의해야한다.우도함수는 이제 세 개의 개념으로 분화된다.
-. 관측된 우도함수 : 현실에서 실현되어 나타난 확률변수들의 우도함수를 의미한다.
$X = [X_{1}, \dots, X_{n}]$를 실현된 확률변수라 할때, 그 우도함수는 아래와 같이 정의한다.
$$L(\theta;X) = g(x|\theta)$$
-. 잠재된 우도함수 : 현실에서 실현되지 않아서 관측이 불가능하지만, 존재함은 알고 있는 확률변수들의 우도함수이다.
$Z = [Z_{1}, \dots, Z_{n}]$.가 관측 불가능 확률변수들의 집합이라 할 떄
$$L(\theta;Z) $$
-. 완전한 우도함수 : 관측된 우도함수와 잠재된 우도함수의 결합 우도함수를 의미한다.
$$L^{c}(\theta;x,z) = h(x,z;\theta)$$
이를 모두 결합하여, 관측된 확률변수가 주어졌을 때 이에 영향을 받는
잠재된 확률변수의 조건부 pdf는 다음과 같이 정의할 수 있다.
$$k(z|\theta, x) = \frac{h(x,z;\theta)}{g(x|\theta}$$- Expectation 단계 : (우리가 관심이 있는) 완전한 우도함수의 기댓값의 꼴을 (구체적인 식으로) 정의하는 것을 Expectation단계(E)라고 한다.
- Maximization 단계 : E단계에서 정의한 완전한 우도함수의 기댓값의 꼴을 최대화하는(= 우도함수를 최대화하는) 모수 $\theta$를 발견하는 것을 maximization 단계라고 한다.
2) 위에서 정의한 우도함수를 결합하여, EM 알고리즘의 첫번째 단계인 Expectation단계를 다음과 같이 유도할 수 있다.
${(1)}$즉, 잠재된 확률변수 Z 조건 하에서 완전한 우도함수 $logL^{c}(\theta|x,z)$의 기댓값의 꼴을 정의하는 것을 E단계라고 한다.관측된 우도함수의 로그우도를 정의하여, 다음과 같은 항등식을 유도한다.
① $\theta$에 대하여 연구자가 추정하는 모수를 $\theta_{0}$라고 정의하자.
$$logL(\theta|X) = \int logL(\theta|X)k(z|\theta_{0},x)dz$$
(이 때, pdf의 정의에 따라 $\int k(z|\theta_{0},x)dz = 1$을 이용하였다)
$L(\theta;X) = g(x|\theta)$이므로 이를 바꿔주면
$$\int log \ g(x|\theta)k(z|\theta_{0},x)dz$$
② 한편, 조건부 pdf $k(z|\theta, x) = \frac{h(x,z;\theta)}{g(x|\theta}$에 로그를 씌워 적절히 변형하면
$log \ g(x|\theta) = log \ h(x,z|\theta) - log \ k(z|\theta,x)$
즉
$$\int log \ g(x|\theta)k(z|\theta_{0},x)dz = \int [log \ h(x,z|\theta) - log \ k(z|\theta,x)]k(z|\theta_{0},x)dz \\ = \int log[h(x,z|\theta)]k(z|\theta_{0},x)dz - \int log[k(z|\theta,x)]k(z|\theta_{0},x)dz$$
한편, 이는 $k(z|\theta_{0},x)$를 pdf로 갖는 조건부 분포 하에서의 기댓값과 같다. 즉
$$E_{(z|\theta_{0},x)}[logL^{c}(\theta|x,z)] - E_{(z|\theta_{0},x)}[log[k(z|\theta,x)]]$$
이 때, 왼쪽의 첫번째 기댓값항
$$Q(\theta|\theta_{0},X) = E_{(z|\theta_{0},x)}[logL^{c}(\theta|x,z)]$$
을 정의하는 것을 EM알고리즘의 첫번째 단계인 Expectation(기댓값) 과정이라고 한다.
3) 한편, 그 다음 단계인 maximization은 다음과 같이 정의할 수 있다.
${(1)}$ 추정 모수 $\theta_{0}$에 대하여, 알고리즘의 m번째 반복에서 도출한 추정 모수 $\theta_{0}$를 다음과 같이 정의하자
-. $\theta_{0}^{m}$: $\theta_{0}$의 m번째 반복에서 추정한 추정모수
${(2)}$ E단계에서 정의한 $Q(\theta|\theta_{0}^{m},X)$을 최대화하는 차세대 모수 $\theta_{0}^{m+1}$를 구하는 것을 Maximization 단계라고 한다. 즉
$$\theta_{0}^{m+1} = argmax(Q(\theta|\theta_{0}^{m},X)$$
${(3)}$ 이 m이 최대한 많이 반복될수록 이는 최대우도추정값으로 확률수렴함을 다음과 같이 보일 수 있다.
${(4)}$ 위 증명의 결과들을 종합하면 아래와 같이 결론내릴 수 있다.$\theta_{0}^{m+1}$는 $Q(\theta|\theta_{0}^{m},X)$ 를 최대화한다고 했으므로, 다음은 참이다.
$$Q(\theta^{m+1}|\theta_{0}^{m},X) \geq Q(\theta^{m}|\theta_{0}^{m},X) \\ = E_{(z|\theta_{0}^{m},x)}[logL^{c}(\theta_{0}^{m+1}|x,z)] \geq E_{(z|\theta_{0}^{m},x)}[logL^{c}(\theta_{0}^{m}|x,z)] \dots ①$$
부등식 양쪽의 기댓값항은 모두 분포 $(z|\theta_{0}^{m},x)$하에서 구해짐에 유의하자
젠센부등식에 따르면, 함수의 기댓값은 기댓값의 함수보다 항상 작거나 같다.
즉, 다음의 사실을 증명 가능하다.
$$E_{(z|\theta_{0}^{m},x)}\begin{bmatrix}
log\frac{k(z|\theta_{0}^{m+1},x)}{k(z|\theta_{0}^{m},x)}
\end{bmatrix}\leq log \ E_{(z|\theta_{0}^{m},x)}\begin{bmatrix}
\frac{k(z|\theta_{0}^{m+1},x)}{k(z|\theta_{0}^{m},x)}
\end{bmatrix}$$
부등식 우변을 적분형식으로 나타내면
$$log \int \frac{k(z|\theta_{0}^{m+1},x)}{k(z|\theta_{0}^{m},x)}k(z|\theta_{0}^{m},x)dz \\= log \int
k(z|\theta_{0}^{m+1},x)dz =log(1) \\ = 0$$
정리하면 아래와 같다.
$$E_{(z|\theta_{0}^{m},x)}\begin{bmatrix}
log\frac{k(z|\theta_{0}^{m+1},x)}{k(z|\theta_{0}^{m},x)}
\end{bmatrix} \leq 0$$
로그를 풀고, 우변으로 이항하면 다음이 성립된다.
$$E_{(z|\theta_{0}^{m},x)}[log \ k(z|\theta_{0}^{m+1},x)]
\leq E_{(z|\theta_{0}^{m},x)}[log \ k(z|\theta_{0}^{m},x)] \dots ②$$
-. 우리의 목적은 $L(\theta|X)$를 최대화 하는것이다. 그리고 $L(\theta|X)$는 다음으로 나타낼 수 있음을 보였다.
$$L(\theta|X) = E_{(z|\theta_{0},x)}[logL^{c}(\theta|x,z)] - E_{(z|\theta_{0},x)}[log[k(z|\theta,x)]]$$
-. 그리고, ①에 따라 $E_{(z|\theta_{0},x)}[logL^{c}(\theta|x,z)]$는 반복 m이 진전될수록 더 큰 값을 갖게 된다.
-. 반면, ②에 따라 $E_{(z|\theta_{0},x)}[log[k(z|\theta,x)]]$는 m이 진전될수록 더 작은 값을 갖게 된다.
-. $m \rightarrow \infty$에 따라 $L(\theta|X)$는 $E_{(z|\theta_{0},x)}[logL^{c}(\theta|x,z)]$에 지배되며, 이를 최대화하는것은 우도함수를 최대화하는것과 동치이다. 그리고, 우도함수가 최대화 된다는것은 $\theta_{0}^{(m)}$이 점차 참모수 $\theta$에 다가감을 의미한다.
4) 위에서 도출한 결론들을 모두 종합하여, EM 알고리즘의 절차를 정의하면 다음과 같다.$\widehat{\theta}^{m}$을 m번째 반복에서의 추정값이라고 하자.
(m+1)번째 반복에서의 추정값을 계산하기 위해, 다음의 두 단계를 시행한다.
1. 기대 단계(Expectation):
완전한 우도함수를 이용하여 기대함수를 정의한다. 즉
$$Q(\theta|\theta_{0},X) = E_{(z|\theta_{0},x)}[logL^{c}(\theta|x,z)]$$
2. 최대화 단계(Maximization)
기대단계에서 정의한 함수를 최대화하는 추정값 $\widehat{\theta}^{m+1}$을 도출한다. 즉
$$\widehat{\theta}^{m+1} = Argmax Q(\theta|\widehat{\theta}^{m},X)$$ - EM 알고리즘의 예시
1) 정규분포 혼합 모델(Gaussian mixture model)
${(1)}$ 클러스터링에 활용되는 GMM도 EM알고리즘의 일종이다. 다음과 같이 유도할 수 있다.$X_{1}$ 을 $N(\mu_{1}, \sigma^{2}_{1})$, 즉 정규분포를 따르는 확률변수라고 하자
$X_{2}$ 을 $N(\mu_{2}, \sigma^{2}_{2})$, 즉 정규분포를 따르는 확률변수라고 하자
또, $W = [W_{1}, W_{2}]$는 $b(n, \epsilon)$인 분포를 따른다고 하자.
1. 기대 단계(Expectation)
다음의 변환 확률변수를 정의한다.
$X = (1 - W)X_{1} + WX_{2}$
즉, 이 확률변수는 베르누이 분포를 따르는 확률변수 W에 따라서 추출된 확률변수가 변하는 혼합 확률변수이다.
그리고, 이 때, W가 관측이 되지 않는 잠재된 확률변수라고 하자.
확률변수 X의 pdf는 다음과 같이 정의할 수 있다.
pdf $f_{x}(x) = (1-\epsilon)f_{x_{1}}(x) + \epsilon f_{x_{2}}(x)$
관측된 우도함수는
$logL(\theta|x) = \sum_{i=1}^{k}log(1-\epsilon)f_{x_{1}}(x_{i}) + \epsilon f_{x_{2}}(x_{i})$
완전한 우도함수는
$$L^{c}(\theta|x,w) = \begin{cases}
\prod_{i=1}^{k}f_{x_{1}}(x_{i}) & \text{ if } w_{i}= 0\\
\prod_{i=1}^{k}f_{x_{2}}(x_{i}) & \text{ if } w_{i}= 1
\end{cases}$$
완전한 우도함수의 로그우도를 구하면
$$l^{c}(\theta|x,w) = \begin{cases}
\sum_{i=1}^{k}log f_{x_{1}}(x_{i}) & \text{ if } w_{i}= 0\\
\sum_{i=1}^{k} log f_{x_{2}}(x_{i}) & \text{ if } w_{i}= 1
\end{cases} \\ = \sum_{i=1}^{k}[(1 - w_{i})log f_{x_{1}}(x_{i}) + w_{i} log f_{x_{2}}(x_{i})]$$
$Q(\theta|\theta_{0},X)$를 정의하면
$$E_{(w|\theta_{0},x)}\begin{bmatrix}
\sum_{i=1}^{k}[(1 - w_{i})log f_{x_{1}}(x_{i}) + w_{i}log f_{x_{2}}(x_{i})]
\end{bmatrix} \\ =
\sum_{i=1}^{k}E_{(w|\theta_{0},x)}(1-w_{i})log f_{x_{1}}(x_{i}) + \sum_{i=1}^{k}E_{(w|\theta_{0},x)}w_{i}log f_{x_{2}}(x_{i})$$
이 때, $E_{(w|\theta_{0},x)}(w_{i})$, 즉 확률변수 W에 조건부 기댓값에 대해 생각해보자.
(그냥 기댓값이 아니라, 조건부 기댓값임에 유의하자)
$$E_{(w|\theta_{0},x)}(w_{i}) = 0 \cdot P[W_{i} = 0|\theta_{0}, X] + 1 \cdot P[W_{i} = 1|\theta_{0}, X] = P[W_{i} = 1|\theta_{0}, X]$$
한편, $P[W_{i} = 1|\theta_{0}, X]$은 잠재된 확률변수 w에 대한 조건부 pdf와 같다. 즉 다음의 관계를 이용할 수 있다.
$$P[W_{i} = 1|\theta_{0}, X] = k(w = 1|\theta, x) = \frac{h(x,w = 1;\theta)}{g(x|\theta)}$$
이를 이용하면 잠재된 확률변수 $w_{i}$의 pdf를 관측된 확률변수의 조건부 pdf로 다음과 같이 나타낼 수 있다.
$$\gamma_{i} = k(w_{i} = 1|\theta,x) = \frac{\widehat{\epsilon} log f_{x_{2}}(x_{i})}{log(1-\widehat{\epsilon})f_{x_{1}}(x_{i}) + \widehat{\epsilon} f_{x_{2}}(x_{i})}$$
$Q(\theta|\theta_{0},X)$로 다시 돌아가면
$$Q(\theta|\theta_{0},X) = \sum_{i=1}^{k}E_{(w|\theta_{0},x)}(1-w_{i})log f_{x_{1}}(x_{i}) + \sum_{i=1}^{k}E_{(w|\theta_{0},x)}w_{i}log f_{x_{2}}(x_{i})$$
$E_{(w|\theta_{0},x)}$는 오직 잠재변수 w에만 의존하는 기댓값 선형자고,
$E_{(w|\theta_{0},x)}(w_{i}) = \gamma_{i}$ 임을 위에서 보였으므로, 이를 이용하여 기댓값 선형자를 정리하면
$$Q(\theta|\theta_{0},X) = \sum_{i=1}^{k}[(1-\gamma_{i})log f_{x_{1}}(x_{i}) + \gamma_{i}log f_{x_{2}}(x_{i})]$$
한편 정규분포의 pdf $f_{x_{1}}, f_{x_{2}}$의 로그변환된 pdf는 다음과 같다.
$$f_{x_{1}} = -log(\sqrt{2\pi})-log(\sigma_{1})-\frac{(x_{1}-\mu_{1})^{2}}{2\sigma_{1}^{2}} \\
f_{x_{2}} = -log(\sqrt{2\pi})-log(\sigma_{2})-\frac{(x_{2}-\mu_{2})^{2}}{2\sigma_{2}^{2}}$$
이를 이용해 Q식을 다시 정리하면
$$Q(\theta|\theta_{0},X) = \sum_{i=1}^{k}[(1-\gamma_{i})-log(\sqrt{2\pi})-log(\sigma_{1})-\frac{(x_{i}-\mu_{1})^{2}}{2\sigma_{1}^{2}} -log(\sqrt{2\pi})-log(\sigma_{2})-\frac{(x_{i}-\mu_{2})^{2}}{2\sigma_{2}^{2}}]$$
2. 최대화 단계(Maxiimzation)
이제 Q식을 이용하여 각각의 모수에 대하여 최대우도추정량을 구한다.
구체적으로는 각 모수에 대해 미분한 후 그 값을 0으로 놓아 방정식을 푼다.
그 결과는 다음과 같다.
$\widehat{\mu_{1}}^{(m+1)} = \sum_{i=1}^{k}\frac{(1-\gamma_{i}^{(m)})x_{i}}{(1-\gamma_{i}^{(m)})}$
$\widehat{\sigma_{1}^{2}}^{(m+1)} = \sum_{i=1}^{k}\frac{(1-\gamma_{i}^{(m)})(x_{i} - \widehat{\mu_{1}}^{(m)})^{2}}{(1-\gamma_{i}^{(m)})}$
$\widehat{\mu_{2}}^{(m+1)} = \sum_{i=1}^{k}\frac{(1-\gamma_{i}^{(m)})x_{i}}{\gamma_{i}^{(m)}}$
$\widehat{\sigma_{2}^{2}}^{(m+1)} = \sum_{i=1}^{k}\frac{\gamma_{i}^{(m)}(x_{i} - \widehat{\mu_{2}})^{2}}{\gamma_{i}^{(m)}}$
한편, 잠재변수 w의 추정값 $\gamma_{i}$는 $E_{(w|\theta_{0},x)}(w_{i})$와 같다.
따라서, $\widehat{\gamma_{i}}$ 는 다음과 같이 다음 반복의 값을 구한다.
$$\widehat{\gamma_{i}}^{(m+1)} = \sum_{i=1}^{k}\frac{\widehat{\gamma_{i}}^{(m)}}{k}$$
3. 알고리즘의 중단 조건
이제, 이 반복 알고리즘을 각각의 반복 m, (m+1) 사이의 우도 함수
$$logL(\theta^{(m)}|x) = \sum_{i=1}^{k}log(1-\gamma^{(m)})f_{x_{1}}(x_{i}) + \gamma^{(m)} f_{x_{2}}(x_{i})$$
증가폭이 일정 Threshold 이하로 내려오면 충분히 수렴되었다 판단하고 알고리즘을 중단한다.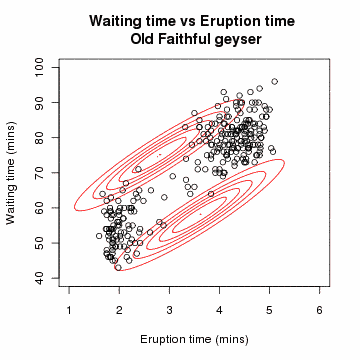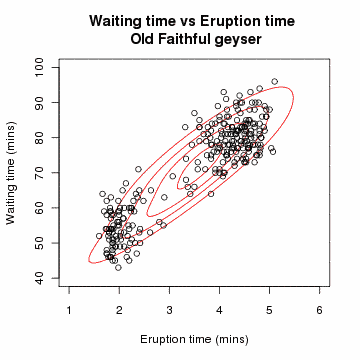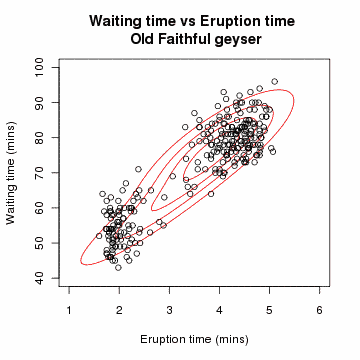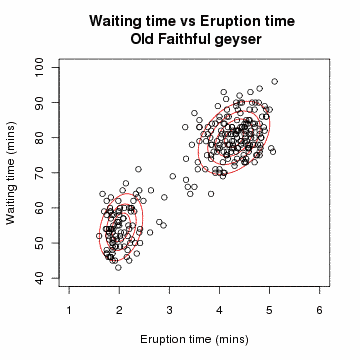
올드페이스풀 간헐천 데이터에 대하여 GMM을 이용한 클러스터링을 시도하는 애니메이션.
임의 초기화된 초깃값으로부터 점차 각각의 군집으로 수렴해가는 형태를 확인할 수 있다.
출처 : 위키피디아
'수리통계' 카테고리의 다른 글
| 34. 완비충분통계량 (0) | 2023.07.24 |
|---|---|
| 33. 충분통계량 (1) | 2023.07.21 |
| 31-1 다중 모수의 최대우도검정 (0) | 2023.07.19 |
| 19-1 다변량 함수에서의 최대우도추정 (0) | 2023.07.18 |
| 31. 최대우도검정 (0) | 2023.07.17 |

